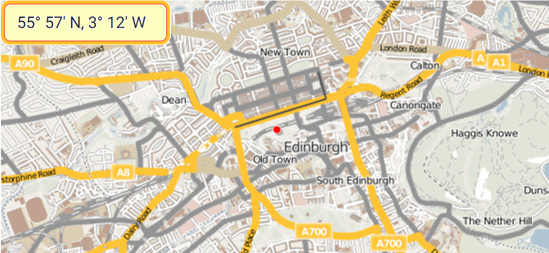
55.95°N, 3.2°W
28° 36' N, 77° 13' E
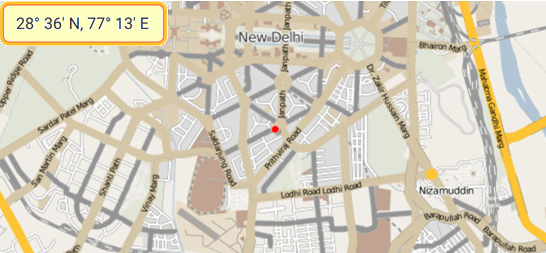
28.6°N, 77.2167°E
Sapendo che la distanza tra due punti P e Q sulla sfera unitaria
è data dall'arcocoseno del prodotto scalare tra P e Q, calcola la distanza
tra Edimburgo
Controlliamo con WolframAlpha se le coordinate sono corrette:


OK
Vediamo anche il valore della distanza che ci fornisce WolframAlpha, per confrontarlo con quello che otterremo noi, ed individuare evantuali errori:
from New Deli to Edimburg 6842 km
|
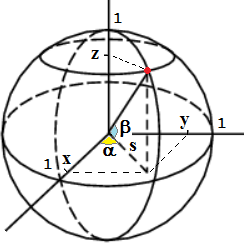
Vediamo come trasformare le coordinate geografiche nelle coordinate cartesiane, ovvero come passare, riferendosi al punto rosso della figura a lato, da α e β ad x, y e z. s = cos(β), z = sin(β), x = cos(α)*s, y = sin(α)*s I nostri dati (trasformati in radianti con "convert degrees in radiant") sono: |
 |
Coordinate cartesiane sulla sfera unitaria:
Edimburgo:
x,y,z: cos(0.05585)*cos(0.9765), sin(0.05585)*cos(0.9765), sin(0.9765)
{0.559053, 0.0312556, 0.828543}
Nuova Deli:
x,y,z: cos(-1.348)*cos(0.4992), sin(-1.348)*cos(0.4992), sin(0.4992)
{0.193993, -0.856265, 0.478723}
dot product
{0.559053, 0.0312556, 0.828543}.{0.193993, -0.856265, 0.478723}
0.478332
Infine:
acos(0.478332) * {6355,6385} → {6812.83, 6844.99}
In base ai calcoli il raggio terrestre starebbe tra i 6812 km e i 6845 km, in accordo col valore dato da WolframAlpha.
Per altri commenti:  lo spazio tridimensionale neGli Oggetti Matematici.
lo spazio tridimensionale neGli Oggetti Matematici.