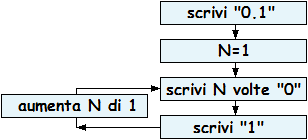
Il diagramma a lato descrive un particolare numero.   Si tratta di un numero razionale o irrazionale?   Perché?

È il numero  0.101001000100001000001…  e così via.
È un numero non periodico, quindi irrazionale, cioè "non razionale", non esprimibile come ratio, ossia come rapporto tra due numeri interi: la divisione tra due interi dà sempre luogo a un numero periodico  ("irrazionale", cioè "non razionale", può significare anche "senza ragione", "privo di ogni logica", ma in questo caso ci si riferisce ad un diverso significato di razionale; in latino, infatti, "ratio" significava sia "ragione", "spiegazione", sia "rapporto", "calcolo"; la parola italiana "ragioniere" deriva anch'essa da questo secondo significato).

Per altri commenti: strutture numeriche neGli Oggetti Matematici

Un altro algoritmo per generare lo stesso numero irrazionale, realizzato con WolframAlpha (vedi).
for n=1 to oo sum(1/10^(n*(n+1)/2))
0.1010010001000010000010000001000000010000000010000000001...

Ed ecco un progrmma in JavaScript:

s="0 . 1"
for(n=1; n<=20; n=n+1) {for(i=1;i<=n;i=i+1) s=s+" 0"; s=s+" 1"}
document.write(s)

0 . 1 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1