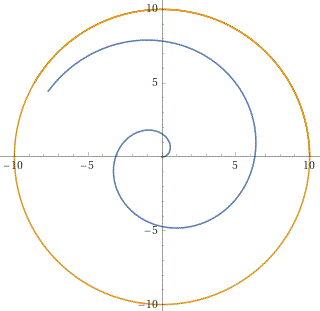
| Se a partire dal centro di una giostra mi dirigo verso il bordo senza mai svoltare, andando dritto, descrivo un segmento. Supponiamo che la giostra si metta in moto e che, da un certo momento, ruoti sempre con la stessa velocità. Se, a questo punto, mi muovessi lungo un raggio della giostra, procedendo sempre con la stessa velocità, quale traiettoria descriverei per una persona che mi veda dall'alto di un palazzo vicino alla giostra? Prima di rispondere fai questo: prendi un foglio di carta, appoggialo su un quaderno, fissane un punto centrale con uno spillo, fai ruotare il foglio più o meno a velocità costante; a questo punto un tuo compagno traccia una linea con una penna a partire dallo spillo, muovendola a velocità costante senza svoltare. Osserva, quindi, la linea che hai descritto. |  |
|
|  |   | x |
Ecco sopra la visione animata di quello che si può vedere. Sotto due visioni non animate. Le figure sono delle spirali, in cui la distanza tra una spira e l'altra è costante (come si vede bene nella seconda figura).
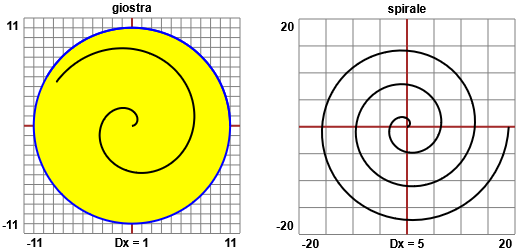
Vediamo più in dettaglio, per gli insegnanti, la questione.
L'uomo si allontana dal centro della piattaforma girevole procedendo in modo rettilineo e con velocità costante, di 0.5 m/s.
Se la piattaforma ha una velocità di rotazione costante, di 10° al secondo, l'uomo, visto dall'alto, descrive la traiettoria a spirale illustrata. Se l'uomo mantenesse la direzione iniziale, che indichiamo con l'asse x, la sua posizione dopo t secondi sarebbe x=0.5t. Se la piattaforma ruota, 0.5t diventa la distanza R dal centro raggiunta dopo t secondi; mentre la direzione α verso cui l'uomo sta puntando diventa Qui e qui puoi vedere gli script con cui sono state realizzate le due immagini. | 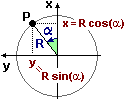 |
Osserviamo che fare questi piccoli esperimenti, che non richiedono molto tempo, è importante perché rimangono impressi nella memoria e saranno, poi, la base per successivi approfondimenti concettuali (la composizione di movimenti contemporanei, i modi in cui descrivere analiticamente le curve, …).
Come realizzare le spirali col software online WolframAlpha:
polar r = t, t = 0..2*pi+5/6*pi
polar r = t, t = 0..6*pi
spiral
 . . .
. . .
La giostra:
parametric plot (t*cos(t), t*sin(t)), parametric plot (10*cos(t), 10*sin(t)), t=0..2*pi+5/6*pi