Altri esercizi sui volumi
Parallelepipedi, cilindri, coni, piramidi
 |
|
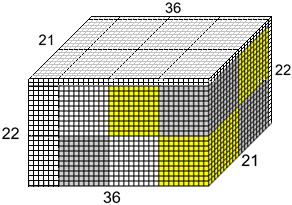
Una scatola come quella disegnata a sinistra, con base rettangolare di dimensioni 36 mm e 21 mm e alta 22 mm,
possiamo pensarla come formata da 22 strati di cubetti uguali con lato di 1 mm, con ogni strato formato da 21 file di 36 cubetti.
I cubetti in tutto sono 36×21×22. Per misurare lo spazio occupato da un oggetto, lo spazio di una stanza, lo spazio contenuto in
un recipiente si usano cubetti di lato 1 mm (i cosiddetti mm³), cubetti di lato 1 cm (i cosiddetti cm³), cubi di lato 1 m (i cosidetti m³), ...
La nostra scatola occupa lo spazio di 36×21×22 mm³. Si dice che ha il volume di 36×21×22 = 16632 mm³.
Come si cede dal disegno, i cubo di lato 1 cm contiene 10×10×10 = 1000 cubetti di lato 1 mm. Quindi 1 cm³ = 1000 mm³. Possiamo allora anche dire che la nostra scatola ha il volume di 16.632 cm³, ossia di quasi 17cm³.
Così come se inclino un rettangolo l'area del parallelogramma ottenuto posso calcolarla sempre facendo base·altezza,
analogamente il volume di un mazzo di carte non cambia se dalla posizione con tutte le carte disposte esattamemte l'una sull'altra lo sposto inclinandolo:
il volume lo posso calcolare in ogni caso moltiplicando l'area di base per l'altezza. Vedi la figura seguente: il volume di questo mazzo di carte è di 116 cm³.
|

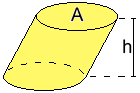 | Analogamente, nel caso in cui la base non sia un rettangolo, il volume si trova sempre moltiplicando l'area di base per l'altezza. Il volume occupato da un liquido si può misurare anche in litri: 1 litro equivale ad un cubo di lato 10 cm, 1 millilitro (1 millesimo di litro) equivale ad 1 cm³. |
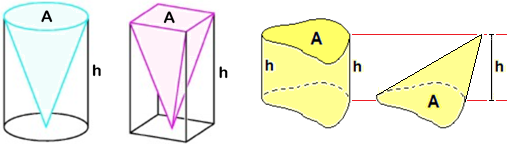
Nel caso delle figure a punta a due dimensioni come i triangoli l'area si trova facendo base·altezza/2 in quanto un triangolo
sta esattamente due volte nel parallelogramma con la stessa base e la stessa altezza.
Nel caso delle figure a punta a tre dimensioni come
i coni e le piramidi il volume si trova facendo area di base·altezza/3.
Volendo potremmo verificare la cosa utilizzando un cono di plastica, riempendolo d'acqua e versandone il contenuto in un cilindro graduato (il volume viene indicato in "ml", ossia in millilitri, che sappiamo essere equiavalenti ai cm³)
|
|  |
01 >>>
02 >>>
03 >>>
04 >>>
05 >>>
06 >>>
Le sfere
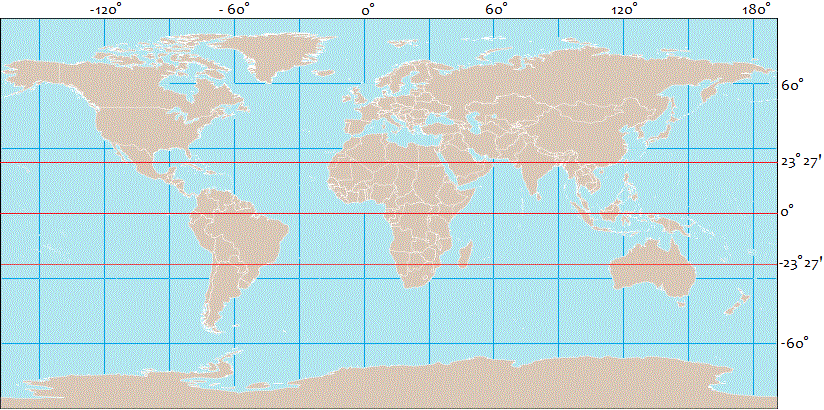
Avrai già visto carte geografiche come quella rettangolare qui sotto a sinistra.
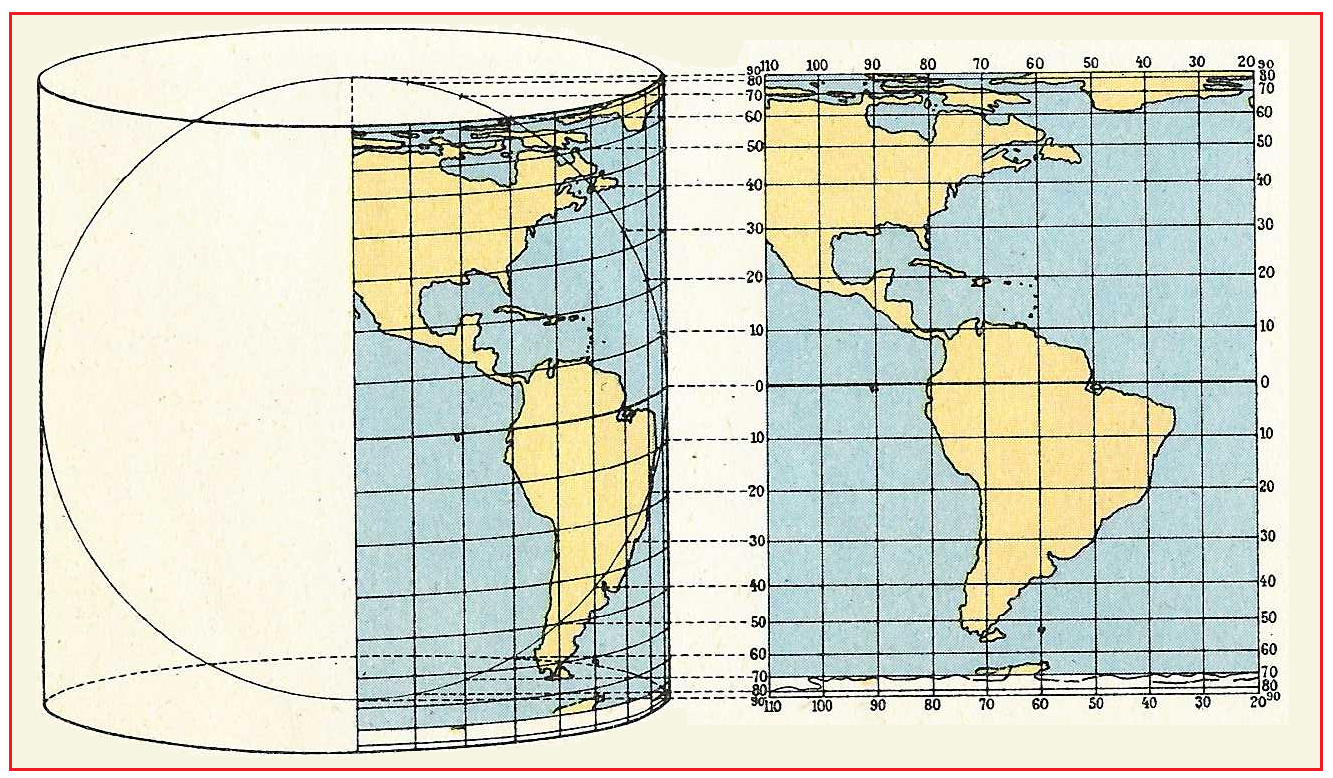
A destra come è stata ottenuta: proiettando i confini dei vari continenti su un cilindro e poi srotolando il cilindro.
Qui puoi vedere le immagini ingrandite.
La caratteristica di questa rappresentazione è che conserva le aree dei vari continenti. In particolare
l'area dell'intera carta è uguale all'area dell'intero globo terrestre. Se vuoi qui trovi una spiegazione di questo fatto.
Dunque la superficie sferica di raggio R equivale alla suferficie latereale del cilindro che ha lo stesso raggio e altezza pari a 2R, ossia vale 2·π·R·2R = 4·π·R².
Per trovare il volume della sfera posso ragionare nel seguente modo.
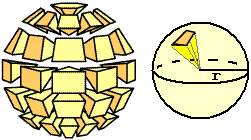
Approssimo la sfera con l'unione di tante piramidi, come illustrato nella figura a fianco.
Al crescere del numero di queste piramidi il volume di
questa unione tende al volume della sfera.
Il volume di ciascuna di queste piramidi, come abbiamo visto all'inizio, è pari
ad un terzo della superficie di base moltiplicata per l'altezza. L'altezza delle piramidi tende a coincidere con il raggio
R della sfera, mentre la somma delle superfici di base tende a coincidere con la superficie totale
della sfera, che abbiamo appena visto come si può calcolare.
Quindi il volume di una sfera di raggio R è Superficie·R/3 =
4·π·R²·R/3 =
4/3·π·R³.
|  |
07 >>>
08 >>>
09 >>>
10 >>>
11 >>>