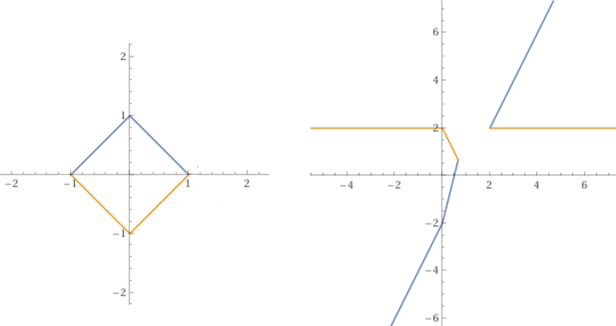
Come viene trasformato il quadrato |x|+|y|=1 da
Sotto la figura e i suoi due
trasformati: un quadrilatero aperto
e illimitato per la trasformazione

Le figure sono state ottenute con WolframAlpha con i comandi:
parametric plot (t, 1-abs(t)), parametric plot (t, -1+abs(t)), t = -1..1
e
parametric plot ( t/(t-1/2),(t+1-abs(t))/(t-1/2) ), parametric plot ( t/(t-1/2),(t-1+abs(t))/(t-1/2) ), t=-1..1
Per commenti, guardare  Prospettiva 2 negli Oggetti Matematici
Prospettiva 2 negli Oggetti Matematici