Scegli tra 1/2 e √2 i valori da dare a q affinché la trasformazione x' = x/(y−x−q), y' = (x+y)/(y−x−q) mandi il cerchio (di centro O e raggio 1) nell'una e nell'altra curva disegnata (pensa a che cosa corrisponde nel piano l'insieme delle coppie (x,y) per cui si annulla il termine a denominatore di x' e y').

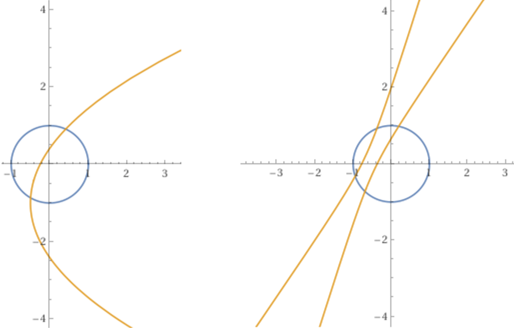
La trasformazione (che è continua) non è definita nei punti del cerchio in cui y−x−q=0, ossia nei punti di intersezione tra cerchio e retta y=x+q. Se q = √2 la retta tocca il cerchio in un punto A (figura sottostante a sinistra); muovendosi sul cerchio man mano che un punto (x,y) si avvicina a A sia x' che y' tendono all'infinito: A viene, in altre parole, trasformato in un punto all'infinito; la curva chiusa iniziale viene trasformata in una curva aperta e illimitata. Se q = 1/2 vi sono due punti di intersezione: questi punti del cerchio sono trasformati in punti all'infinito, e il cerchio viene trasformato in 2 archi illimitati. Se q>√2 non vi sono intersezioni e il cerchio viene trasformato in una curva chiusa; lo stesso accade per q<√2 (figura sottostante a destra). Le immagini del cerchio, nei tre casi, sono una parabola, un'iperbole e un'ellisse. I punti all'infinito corrispondono alla direzione dell'asse della parabola (la direzione a cui si tende sulla parabola allontanandosi dal vertice) e alle direzioni dei due asintoti dell'iperbole.

             

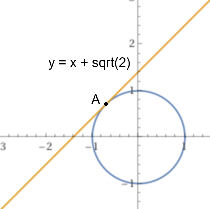
Per commenti, guardare Prospettiva 2 negli Oggetti Matematici