• A destra sono raffigurate una struttura a forma di quadrato suddiviso in quattro quadrati disposta orizzontalmente e la sua ombra proiettata dai raggi del sole su una superficie piana verticale.  I raggi del sole formano angoli di 45° con tale superficie; la disposizione è tale che l'ombra ha la stessa forma della struttura. Sulla quadrettatura seguente è riprodotta la struttura.  Disegna (con la stessa scala di riproduzione) come sarebbe l'ombra se il sole fosse più alto e i suoi raggi formassero angoli di 30° con la verticale  (usa un opportuno funzione trigonometrica per calcolare le dimensioni con cui disegnare l'ombra).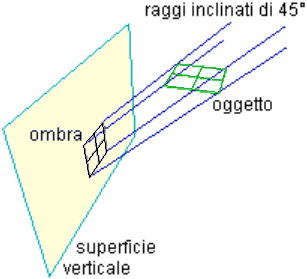

• Traccia su un'analoga quadrettatura l'ombra della stessa struttura che una lampadina (non schermata) posta 30 cm sopra il centro della struttura proietterebbe su una superficie piana orizzontale posta 15 cm sotto alla struttura.

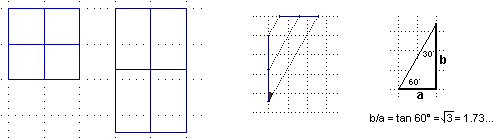
• Nel caso in cui i raggi del sole formino angoli di 30° l'ombra è allungata rispetto al reticolato di un fattore pari a tan 60° = √3;  anche senza usare funzioni trigonometriche si poteva arrivare a questa conclusione applicando il teorema di Pitagora al triangolo rettangolo con angoli di 60 e 30 gradi e osservando che (essendo questo metà di un triangolo equilatero) il suo cateto minore è metà dell'ipotenusa:  se a è lungo 1, l'ipotenusa è lunga 2 e, quindi, b è lungo √(2² − 1²) = √3.

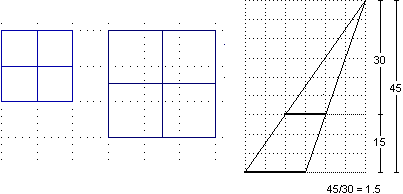
• L'ombra ha stessa forma del reticolato e dimensioni pari a 1 volta e mezza quelle di esso: infatti ogni coppia di raggi di luce che passa per il reticolato forma con il piano del reticolato e con il piano dell'ombra due triangoli dalla stessa forma ma con "altezze" (rispetto ai segmenti che stanno su questi due piani) lunghe rispettivamente 30 cm e 45 cm; dello stesso fattore di ingrandimento (45/30 = 1.5 = 150%) viene ingrandito il segmento di "base". Non è necessario che la lampadina sia sopra al centro della struttura.

Per eventuali approfondimenti vedi la voce "proiezioni tra superfici" negli Oggetti Matematici.