Un modo alternativo per descrivere parabole, ellissi ed iperboli.
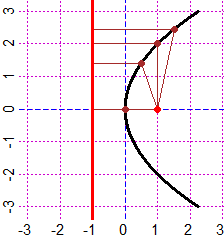
(a)  Una parabola è l'insieme dei punti del piano equidistanti da un punto (detto fuoco) e una retta (detta direttrice) fissati.  Scrivi l'equazione della parabola che ha fuoco (q,0) e direttrice x = -q.
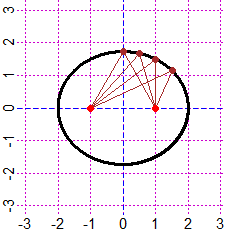
(b)  Una ellisse è l'insieme dei punti del piano le cui distanze da due punti fissati (detti fuochi) hanno somma costante.  Scrivi l'equazione della ellisse che ha fuochi (q,0) e (-q,0) e somma delle distanze da essi dei suoi punti pari a k.
(c)  Una iperbole è l'insieme dei punti del piano le cui distanze da due punti fissati (detti fuochi) hanno differenza costante.  Scrivi l'equazione della iperbole che ha fuochi (q,0) e (-q,0) e differenza delle distanze da essi dei suoi punti pari a k.

Vedi qui se vuoi rivedere come le coniche possono essere ottenute sia intersecando un cono con un piano che come grafico di generiche equazioni polinomiali in x,y di 2º grado.  Qui vedi anche come possono essere descritte in forma polare.  Qui vedi vari modi di tracciarle con WolframAlpha.

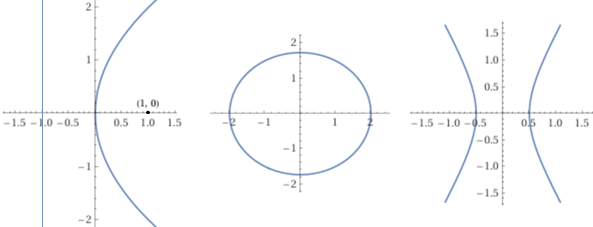
Ecco sotto come ottenere le figure richieste dal quesito tracciate con WolframAlpha bei casi in cui   (a) q=1  [parabola focus (1,0) and directrix x = -1  −  o:  y^2 = 4*1*x],   (b) q=1, k=4  [sqrt((x-1)^2+y^2)+sqrt((x+1)^2+y^2)=4],   (c) q=1, k=1  [abs(sqrt((x-1)^2+y^2)-sqrt((x+1)^2+y^2))=1]: