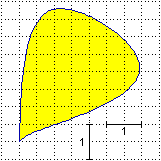
Misura (approssimativamente) l'area della figura a sinistra (indica la precisione della misura che hai effettuato)
| | Misura (approssimativamente) l'area della figura a sinistra (indica la precisione della misura che hai effettuato) |
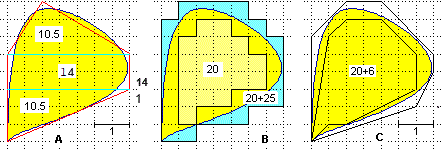
| Vi sono varie strategie. Quella raffigurata sotto in A consiste nell'approssimare il contorno con una figura poligonale e nel valutare l'entità dell'errore considerando quanto le parti indebitamente incluse compensano quelle escluse: l'area del poligono è 35 quadretti; l'errore si può stimare in al più 2 quadretti; quindi l'area sarebbe 35±2 quadretti; poichè un quadretto ha area 1/4, l'area è 8.75±0.5. Il metodo illustrato in B è più semplice: l'area è compresa tra 20 e 45 quadretti, cioè tra 5 e 11.25 (non contrasta con la precedente valutazione: questo intervallo di misure include il precedente). Il metodo in C cerca di precisare le valutazioni per difetto ed eccesso fatte in B considerando e mettendo insieme anche frazioni di quadretto (la parte interna verrebbe 26 quadretti, cioè 6.5; anlogamente si può valutare l'area del poligono contenitore). |
 |
|
Ma avrei potuto anche triangolare la figura e ricavare le aree dei triangoli dalle lunghezze dei lati. Per calcolare le aree dei triangoli posso ricorrere allo script "tri lato-lato-lato"
presente qui
ottenendo 1.6393119745796, 2.2211483516416 e 4.2, la cui somma è 8.0604603262212, arrotondabile a 8.1. |  |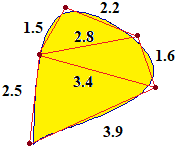
Per calcolare le aree dei triangoli posso ricorrere allo script "tri lato-lato-lato"
presente qui
ottenendo 1.6393119745796, 2.2211483516416 e 4.2, la cui somma è 8.0604603262212, arrotondabile a 8.1. Ovvero posso utilizzare
WolframAlpha:
area triangle (1.5,2.2,2.8) → 1.63931 area triangle (3.4,1.6,2.8) → 2.22115 area triangle (3.4,2.5,3.9) → 4.2
1.63931 + 2.22115 + 4.2 → 8.06046 (che arrotondo a 8.1).
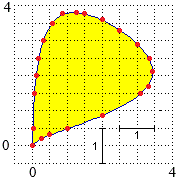
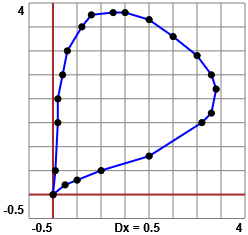
Per una approssimazione migliore posso utilizzare lo script "area polig" che mi consente di calcolare l'area di un poligono di cui siano note le coordinate dei vertici. Approssimo il contorno della figura con i punti sotto tracciati, aventi come "x" e come "y" i seguenti valori:
0, 0.25, 0.5, 1, 2, 3.1,3.3,3.4, 3.3, 3, 2.5, 2, 1.5,1.25, 0.8, 0.6,0.3, 0.2, 0.1, 0.1,0.05, 0 0, 0.2, 0.3, 0.5,0.8, 1.5,1.7,2.2, 2.5,2.9, 3.3,3.65, 3.8, 3.8, 3.8, 3.5, 3, 2.5, 2, 1.5, 0.5, 0
|
Ottengo 8.38875 che arrontondo a 8.4. Questa è un'ottima approssismazione dell'area del nostro poligono. Volendo controllare se ho messo i dati giusti traccio un poligono che abbia i vertici con queste coordinate (vedi qui lo script con cui è stata realizzata la figura). L'esito mi conferma la correttezza dei dati introdotti. |
 |
Per altri commenti: 
approssimazioni, calcolo approssimato e area neGli Oggetti Matematici.