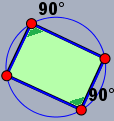
A fianco è raffigurato un rettangolo inscritto in un cerchio. La somma delle ampiezze di due angoli opposti è 180°.  Verifica (eventualmente utilizzando del software) se questa proprietà si mantiene per qualunque quadrilatero inscritto.

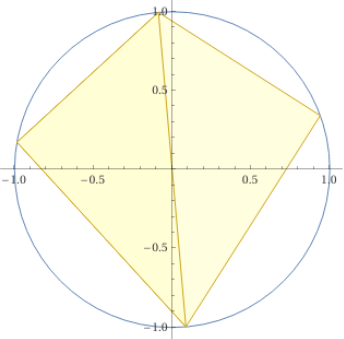
È facile osservare che, oltre che nel caso dei rettangoli inscritti, la proprietà vale anche negli altri casi in cui due vertici non consecutivi sono gli estremi di un diametro, come nelle situazioni illustrate nelle due figure sottostanti a sinistra.  Anche gli altri due angoli hanno come somma 180°, in quanto la somma delle ampiezze dei 4 angoli deve essere pari a 2 angoli piatti (vedi).

     

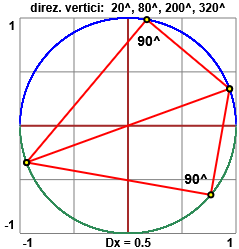
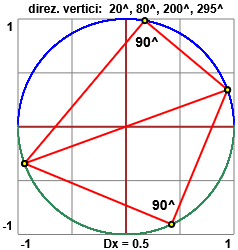
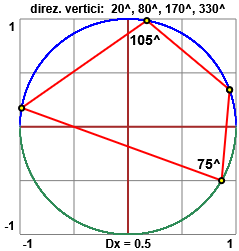
Sia tracciando le figure con la penna e misurando gli angoli col goniometro sia che operando col computer possiamo capire che anche negli altri casi (vedi la terza figura soprastante) la somma delle ampiezze degli angoli opposti è 180°.

Posso verificare la cosa facilmente anche con WolframAlpha:

circle(1,0),(0,1),(-1,0), polygon((cos(20°),sin(20°)),(cos(80°),sin(80°)),(cos(170°),sin(170°)),(cos(330°),sin(330°)))

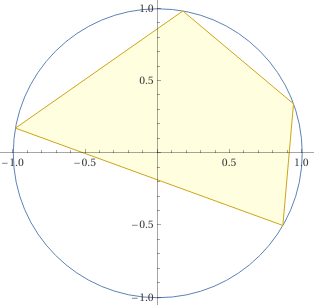
polygon((cos(20°),sin(20°)),(cos(80°),sin(80°)),(cos(170°),sin(170°)),(cos(330°),sin(330°)))

2.182 + 0.960 = 3.142     1.833+1.309 = 3.142

Nonostante l'evidenza, come dimostrare l'equivalenza, per un quadrilatero, di avere angoli opposti di ampiezze che hanno per somma 180° e di essere inscrivibile in un cerchio?
Sappiamo che (vedi) tutti gli angoli inscritti in un cerchio che intercettano su esso lo stesso arco hanno la stessa ampiezza.  Quindi posso ricondurre ad esempio la configurazione sopra raffigurata alla seguente, spostando il vertice superiore e il vertice inferiore.  Siamo in una situazione analoga a quella della prima figura, all'inizio della pagina!

polygon((cos(20°),sin(20°)),(cos(95°),sin(95°)),(cos(170°),sin(170°)),(cos(275°),sin(275°)))

Gli script con cui sono state costruite le figure iniziali:  uno,  due,  tre