Trova un punto equidistante dai tre punti (0,0), (3,4) e (-1,2).

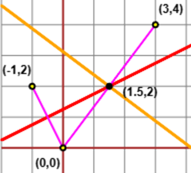
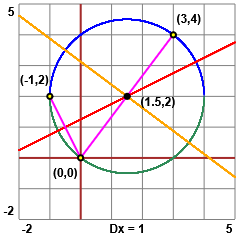
Basta fare l'intersezione degli assi di due segmenti che hanno punti tra i precedenti come estremi. Conviene prendere i due segmenti che hanno (0,0) come estremo. L'asse di uno ha equazione:  (x-0)^2+(y-0)^2=(x+1)^2+(y-2)^2, da cui 2x+1-4y+4=0, ossia 2x-4y+5=0. Quello dell'altro ha equazione:  (x-0)^2+(y-0)^2=(x-3)^2+(y-4)^2, da cui -6x+9-8y+16=0, ossia 6x+8y-25=0. 4y = 2x+5, 6x+4x+10-25 = 0 x = 15/10 = 3/2, y = 8/4 = 2.

Sarebbe stato molto più dispendioso risolvere il problema trovando il cerchio che passa per i tre punti.  Con software che abbia incorporati gli opportuni algoritmi si sarebbe ovviamente proceduto più facilmente in questo modo.  Ecco, a sinistra, che cosa si sarebbe ottenuto con lo script "cerchio 3P" presente qui.

Un'immagine completa del contesto (realizzata con questo script) →