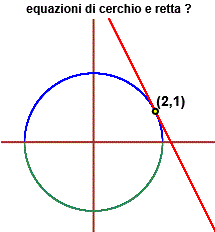
| Nella illustrazione a lato la retta è tangente al cerchio. Scrivi le equazioni della retta e del cerchio. |

|
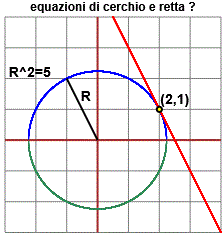 | (2,1) è il punto comune a retta e cerchio. Gli altri punti (x,y) del cerchio distano dal centro O = (0,0) quanto dista (2,1). Quindi il cerchio ha equazione: x2 + y2 = 22 + 12, ossia: La retta è perpendicolare al raggio passante per (2,1).
Questo ha pendenza 1/2, quindi la retta ha come pendenza l'opposto del reciproco di questo valore, ossia –2. y = –2x + 5 |
Ovvero la retta passante per (2,1) con pendenza −2 è la retta con la stessa pendenza passante per (0,0) spostata a destra di 2 e alzata di 1:
y = −2·x → y = −2·(x−2)+1 = −2·x + 5
Volendo, si poteva ragionare "algebricamente", ad es. così:
la nostra retta deve passare per (2,1), ossia all'input x=2 deve corrispondere l'output y=1,
ossia –2·2 + k deve essere uguale a 1:
2·2 + k = 1 → k = 1 + 2·2 → k = 5 Quindi la retta è y = –2x + 5.
Posso controllare la risposta con WolframAlpha battendo "tangent to x^2+y^2=5 at (2,1)" (vedi); ottengo: y = 5 − 2x
Per commenti:  figure(2) neGli Oggetti Matematici
figure(2) neGli Oggetti Matematici
Gli script con cui sono state ottenute le immagini precedenti:
uno e due