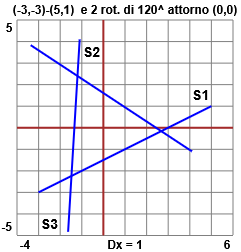
Disegna su un sistema momometrico il segmento S1 di estremi (-3,-3) e (5,1).  Sia S2 il segmento ottenuto applicando a S1 la rotazione di 120° attorno a (0,0).  Sia S3 il segmento ottenuto applicando la stessa trasformazione a S2.  Che figura è la parte limitata di piano racchiusa da questi 3 segmenti?

120 = 360/3: si ottiene un triangolo equilatero →

L'immagine è stata ottenuta con questo script, nei cui comandi si è tenuto conto che la rotazione attorno a (0,0) dell'angolo ampio α è

(x, y)  →  (x*cos(α) - y*sin(α),  x*sin(α) + y*cos(α))

e che  cos(120°) = -1/2,  per cui la roazione di 120° è:

(x, y)  →  (-x/2 - y*sin(120°),  x*sin(120°) - y/2)