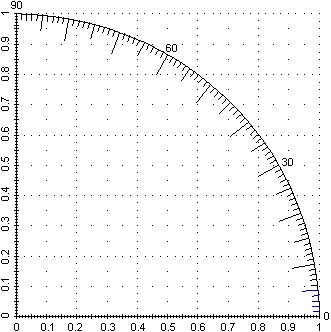
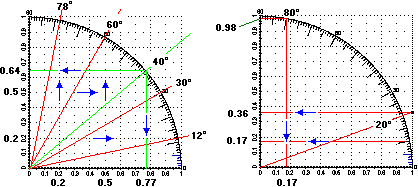
Utilizzando il quarto di goniometro qui a destra determina (mostrando procedimenti, e ragionamenti):

1) le direzioni del versore con componente verticale positiva avente 0.5 come componente orizzontale e di quello avente 0.2 come componente orizzontale,
2) le direzioni dei versori con componenti orizzontali positive aventi i valori precedenti come componenti verticali,
3) i versori di direzioni 40°, 130°, 220°, –40°,
4) cos(80°), sin(10°), cos(190°),
5) tan(160°), tan(70°).

1) la retta x=0.2 taglia il cerchio vicino alla tacca 78°, la retta x=0.5 lo taglia vicino alla (anzi sulla) tacca 60°
2) posso considerare le rette y=0.2 e y=0.5, oppure osservare che, per simmetria, le direzioni sono pari a 90° meno quelle trovate sopra: (90–78)°, (90–60)°.

3) il raggio che passa per la tacca 40° taglia il cerchio nel punto di coordinate, approssimate, x=0.77, y=0.64; il versore di direzione 130° (=90°+40°) lo taglia in x=–0.64, y=0.77; il versore di direzione 220° (=180°+40°) lo taglia in x=–0.77, y=–0.64; il versore di direzione –40° lo taglia in x=0.64, y=–0.77
4) la tacca 80° corrisponde a x=0.17; la tacca 10° corrisponde a y=0.17 (per simmetria, è lo stesso valore); a 190° = 180°+10° corrisponde come x l'opposto di quella corrispondente a 10°, ovvero la y corrispondente a 80°: 0.98

5) la pendenza di 160° = 180°–20° è la stessa di –20°, ossia l'opposto di quella di 20°: –0.36; per 70° (se non voglio prolungare la retta verticale tangente al cerchio) posso procedere trovando cos e sin e farne il rapporto, oppure posso osservare che 70° = 90°–20°, e fare il reciproco di tan(20°), ossia 1/0.36.

Per altri commenti: direzioni e funz. circolari e trasf. geometriche neGli Oggetti Matematici.

1) la retta x=0.2 taglia il cerchio vicino alla tacca 78°, la retta x=0.5 lo taglia vicino alla (anzi sulla) tacca 60° 2) posso considerare le rette y=0.2 e y=0.5, oppure osservare che, per simmetria, le direzioni sono pari a 90° meno quelle trovate sopra: (90–78)°, (90–60)°.
3) il raggio che passa per la tacca 40° taglia il cerchio nel punto di coordinate, approssimate, x=0.77, y=0.64; il versore di direzione 130° (=90°+40°) lo taglia in x=–0.64, y=0.77; il versore di direzione 220° (=180°+40°) lo taglia in x=–0.77, y=–0.64; il versore di direzione –40° lo taglia in x=0.64, y=–0.77
4) la tacca 80° corrisponde a x=0.17; la tacca 10° corrisponde a y=0.17 (per simmetria, è lo stesso valore); a 190° = 180°+10° corrisponde come x l'opposto di quella corrispondente a 10°, ovvero la y corrispondente a 80°: 0.98
5) la pendenza di 160° = 180°–20° è la stessa di –20°, ossia l'opposto di quella di 20°: –0.36; per 70° (se non voglio prolungare la retta verticale tangente al cerchio) posso procedere trovando cos e sin e farne il rapporto, oppure posso osservare che 70° = 90°–20°, e fare il reciproco di tan(20°), ossia 1/0.36.