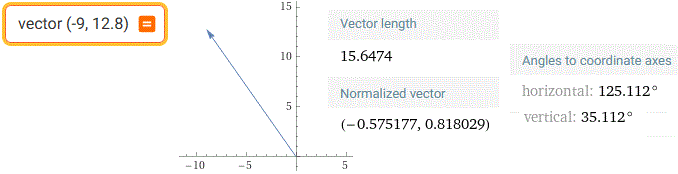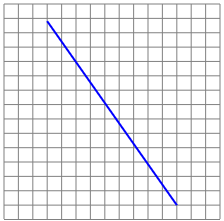
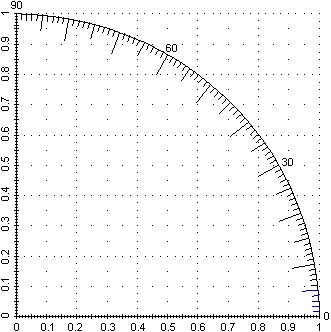
Determina il versore del vettore rappresentato nel sistema di riferimento monometrico sottostante a sinistra.  Utilizza opportunamente l'immagine riportata a destra.

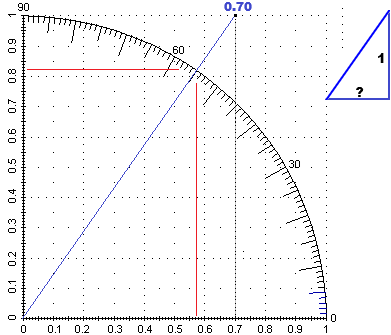Cerco di determinare un triangolo con ipotenusa inclinata come il vettore e con cateto verticale lungo 1, in modo da poterlo disegnare sul quarto di goniometro. Il vettore ha componenti proporzionali a 9 (orizzontale) e a 12.8 (verticale).     1/x = 12.8/9,  x = 9/12.8 = 0.703125 Traccio il segmento che congiunge (0,0) e (0.70,1).  Trovo che l'angolo è quasi esattamente 55° e che le componenti del versore sono circa 0.575 e 0.82.

Ma il vettore originale era ribaltato, per cui (dato che 90-55+90 = 125) la sua direzione è 125° e le componenti del suo versore sono circa -0.575 e 0.820 (o, meglio, -0.575 e 0.820 con la precisone di 0.002).

In alternativa, conoscendo le funzioni circolari, avrei potuto calcolare atan(–12.8/9)+180° ottenendo 125.112…°, che avrei arrotondato a 125°, e per trovare le componenti del versore avrei potuto calcolare cos(atan(–12.8/9)+180°) e sin(atan(–12.8/9)+180°) ottenendo -0.57517… e 0.81802… che avrei arrotondato a -0.575 e 0.818.

Per altri commenti: direzioni e funz. circolari neGli Oggetti Matematici.

Come controllare le risposte con WolframAlpha:

The normalized vector, or unit vector ("versore" in italiano), is in the same direction but has length 1