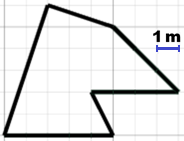
A lato è riprodotta una cartina che rappresenta un campo.  Suddividendo opportunamente il poligono in triangoli e rettangoli derminane l'area.  Poi utilizzando lo script "area polig" presente qui controlla il valore dell'area e determina quello del perimetro. Con lo script "triangolo rettangolo" (con "cateto cateto") determinane anche lati ed angoli.  Le lunghezze arrotondale ai centimetri, l'area ai dm², gli angoli ai decimi di grado.

A destra uno dei possibili modi in cui è suddivisibile il campo. L'area: 3·3 + 2·2 + 3·3/2 + 2·6/2 + 2·1/2 + 3·1/2 = 13 + (9+12+2+3)/2 = 13+26/2 = 26 (m²).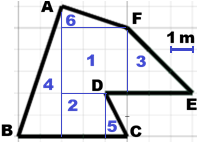

Con lo script "area polig":

Ho la conferma che l'area è di 26 m². Il perimetro è 24.96554164512421, arrotondando 24.97 metri.

Con "triangolo rettangolo" ("cateto cateto") applicato al rettangolo 4, L2=6, L3=2, ho  AB=L1=6.324555320336759, A1=90, A2=71.565051177078, A3=18.434948822922. Quindi AB = 6.32 m, ∠CBA = 71.6°. Triangolo 3. L2=L3=3, ho  L1=4.242640687119285, A1=90, A2=A3=45. Quindi EF = 4.24 m, ∠FED = 45°. Triangolo 5. L2=2, L3=1, ho  L1=2.23606797749979, A1=90, A2=63.434948822922, A3=26.565051177078. Quindi CD = 2.24 m, ∠DCB = 63.4°. Triangolo 6. L2=3, L3=1, ho  L1=3.1622776601683795, A1=90, A2=71.565051177078, A3=18.434948822922. Quindi AF = 3.16 m.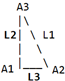

BC = 5 m, DE = 4 m, ∠BAF = 18.434948822922+71.565051177078 = 90° (ma potevamo osservare subito che i triangoli con ipotenuse AB e AF sono simili), ∠EDC = 270+26.565051177078 = 296.6°, ∠AFE = 18.434948822922 + 90 + 45 = 153.4°.

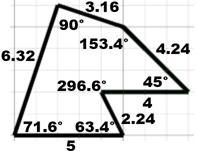Contolliamo il perimetro: 6.32+4.24+2.24+3.16+4+5 = 24.96;  OK (la differenza da 24.97 è dovuta agli arrotondamenti). Calcoliamo anche la somma degli angoli: 90+153.4+45+296.6+63.4+71.6 = 720;  Un poligono a 6 lati è suddivisibile in 4 triangoli (BDC, BDA, ADF, FDE); la somma degli angoli è dunque 180·4 = 720°. OK!

Il disegno del campo è stato tracciato con lo script "lapisA" (vedi qui) con i comandi  11111pcbbq01111666pcccbqpccddddddq0