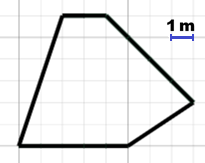
| A lato è riprodotta una cartina che rappresenta un campo. Utlizzando opportuno software determina perimetro, area, lati ed angoli del campo, arrotondati ai centimetri, ai dm² e ai decimi di grado. |  |
Con lo script "area polig" presente qui, introdotte le ascisse e le ordinate dei vertici del campo (riprodotto sotto dando dei nomi ai vertici), trovo:
|
y: 0,0,2,6,6,0 perim = 22.58696084529313 area = 31 | 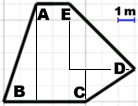 |
perimetro = 22.59 m, area = 31.00 m²
I lati orizzontali del campo sono lunghi AE = 2 m e BC = 5 m.
Il lato sinistro AB lo trovo con lo script "triangolo rettangolo" considerando il triangolo con cateto orizzontale di 2 m e quello verticale di 6 m:

AB = 6.32 m. Trovo anche che l'angolo BAE è 90°+18.4349488...°, ossia 108.4°, e che ∠ABC = 71.565051...°, ossia 71.6°.
Con lo stesso script applicato ai triangoli rettangoli con ipotenuse ED e CD trovo che
ED = 5.656854249492381 m, arrotondando 5.66 m; altri angoli ampi 45°
CD = 3.605551275463989 m, arrotondando 3.61 m; altri angoli ampi 33.6900675259798°, 56.3099324740202°, arrotondando 33.7°, 56.3°.
∠EDC = 33.7+45 = 78.7°, ∠DCB = 90+56.3 = 146.3°.
Controlliamo il perimetro: 2+5+5.66+3.61+6.32 = 22.59, in accordo col valore ottenuto con il primo script.
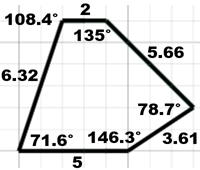
Negli ultimi anni delle scuole superiori vedrai come si potrebbero determinare questi valori senza utilizzare programmini come questi.
Il disegno del campo è stato tracciato con lo script "lapisA" (vedi qui) con i comandi 11111paaabbq0666633pccddddddq0