Una torre alta 40 m proietta un'ombra di 24 m.
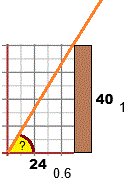
Qual è l'altezza del sole? Rispondi usando la figura a lato, tenendo conto che 24/40 = 0.6.
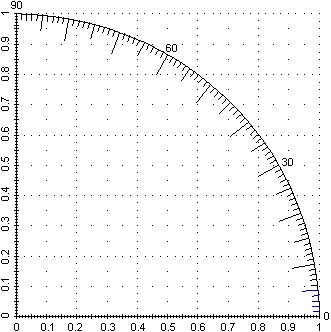
Una torre alta 40 m proietta un'ombra di 24 m.
Qual è l'altezza del sole? Rispondi usando la figura a lato, tenendo conto che 24/40 = 0.6. |

|
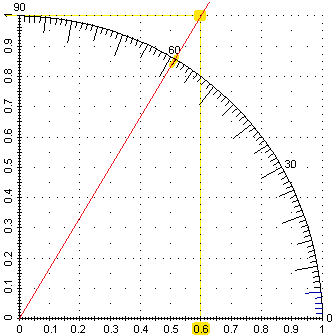 |

|
Posso concludere che l'altezza del sole è tra 58° e 60°, ovvero (59±1)°
Se conosco già la funzione "tangente" (tan), che dato un angolo α, calcola la pendenza di una semiretta diretta come α, posso calcolarne la funzione inversa "arcotangente" (atan). Uso la "calcolatrice" presente qui:
Ovvero l'altezza del sole è tra 58.19° e 59.88°, o tra 58° e 60°
Per altri commenti:  pendenze e curve di livello neGli Oggetti Matematici
pendenze e curve di livello neGli Oggetti Matematici