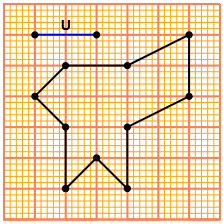
A lato è riprodotta la rappresentazione cartografica su carta millimetrata della base di un castello che ha un'estensione di 1200 m2. Qual è la scala di riduzione della cartina? Ovvero quale è la lunghezza U che rappresenta un segmento lungo 1 cm?

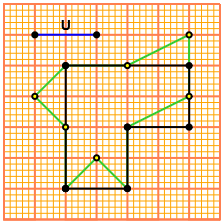
Come evidenzia l'immagine a lato, mediante lo spostamento di tre riangoli si ottiene una figura equivalente che ha l'estensione di 3 cm².  Quindi 3 cm² sulla carta rappresentano 1200 m², ovvero 1 cm² rappresenta 400 m².  Un quadrato di area 400 m² ha lato di 20 m (√400=20).  Quindi 1 cm sulla carta rappresenta U = 20 m.  20 m = 20·100 cm = 2000 cm.  La figura è quindi 1/2000 della realtà:  1/2000 (ovvero 1:2000 ovvero 0.0005) è la scala di riduzione. Si poteva arrivare alla soluzione anche procedendo così: DistanzaReale/DistanzaSuCarta = √(AreaReale/AreaSuCarta) = √(1200 m²/ 3 cm²) = √(12000000 cm²/ 3 cm²) = √(4000000) = 2000.

Sui fattori di scala e sulla proprietà additiva: diagrammi e area neGli Oggetti Matematici.

Le figure sono state realizzate, facilmente, con questi script:  uno  e  due