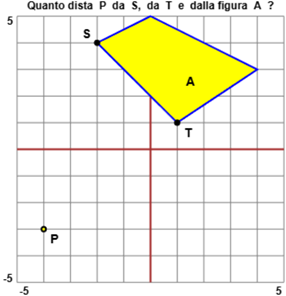
Quanto vale la distanza dal punto P dal punto S e dal punto T?  Quanto vale la dista del punto P dalla figura A?

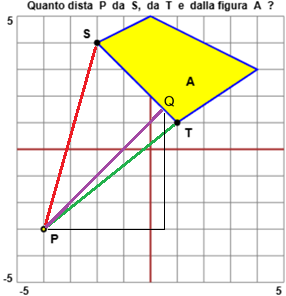Col teorema di Piatgora, PS = √(2²+7²) = √53 = 7.28010988928...,  PT = √(5²+4²) = √41 = 6.40312423743... La distanza di P dalla figura A è il modo più breve per andare da P ad A, ossia è la lunghezza del più piccolo segmento che va da P ad un punto che sta nella figura. Il punto della figura A più vicino a P è il punto Q che si ottiene tracciando da P la perpendicolare al segmento più vicino del contorno di A, ovvero dal segmento ST. In questo caso è tutto facile:  ST passa per le diagonali dei quadretti che attraversa,  PQ passa dunque per le diagonali dei quadretti che attraversa che sono perpendicolari alle precedenti. PQ = √(4.5²+4.5²) = √40.5 = 6.36396103067..., giustamente un po' più corto di PT. Potevo calcolare anche PQ come il prodotto della diagonale di un quadratino per 4 e 1/2:  √2·4.5 = 1.414213562373·4.5 = 6.36396103067...