Gli antichi Romani per misurare l'estensione delle superfici agrarie le scomponevano in figure semplifici di cui calcolavano le aree, che poi sommavano. Una figura spesso usata era il triangolo equilatero, per il quale, se il suo lato era K, assumevano come area K²/2. Che errore commettevano?
|
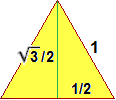
Vediamo come calcolare esattamente l'area di un triangolo equilatero con lato lungo 1. Traccio passando per un vertice una altezza del triangolo. Essa lo divide in due triangoli rettangoli aventi l'ipotenusa lunga 1 e un cateto lungo 1/2. L'altezza del triangolo è la lunghezza dell'altro cateto, che trovo impiegando il teorema di Pitagora: Quindi l'area è base·altezza/2 = 1· Per il triangolo equilatero di lato K usavano K²·0.5 invece di K²·0.4330127… Gli architetti romani non facevano queste grossolane approssimazioni. |  |
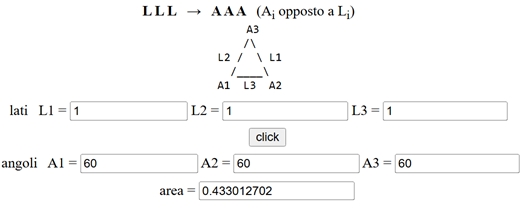
Potevamo anche usare lo scripi "tri lato-lato-lato" (vedi QUI), trovando:
