Traccia le tre perpendicolari innalzate nei punti medi dei lati di questo triangolo, rappresentato a fianco in forma ridotta.  Che cosa puoi osservare?

 

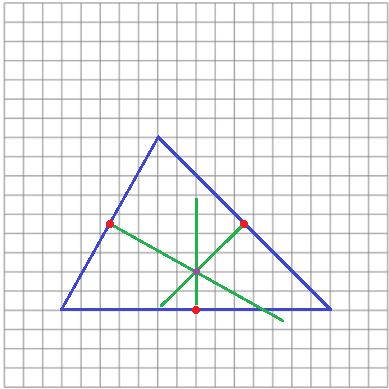
Abbiamo tracciato le perpendicolari utiizzando la quadrettatura. Per il lato orizzontale è facile.  Per il lato sinistro, che va a destra di 5 e sale di 9, traccio un segmento che andando a destra di 9 scende di 5.  Per quello destro, che passa per le diagonali dei quadretti, ne traccio uno che passa per le diagonali dei quadretti perpendicolari alle precedenti.  Posso osservare che tutte e tre le perpendicolari passano per uno stesso punto.
Posso osservare qualcosa in più?
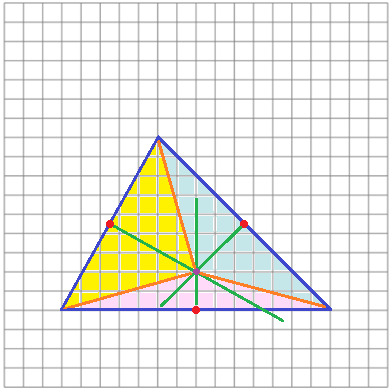
Se congiungo questo punto con i vertici ottengo tre triangoli che sono isosceli in quanto ciascun triangolo è diviso dalla perpendicolare in due triangoli rettangoli con due cateti uguali e che sono quindi uguali. Vedi la figura sottostante a sinistra.
Posso fare qualche altra osservazione.
I nuovi lati (di colore arancione) sono tra loro uguali, quindi posso tracciare il cerchio con centro nel loro punto di incontro e che passa per i vertici del triangolo. Vedi la figura sottostante a destra.

 

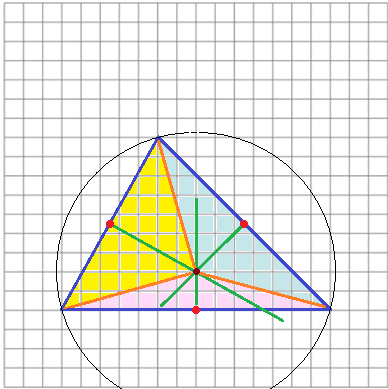
Abbiamo scoperto come si può tracciare il cerchio che passa per tre punti: basta considerare il triangolo che li ha come verici e prendere come centro del cerchio l'intersezione delle rette perpendicolari ai lati e che passano per i loro punti medi.