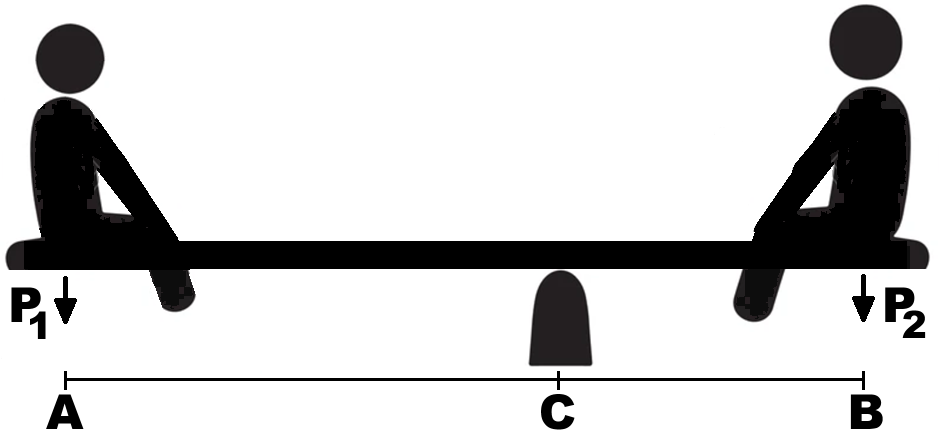
Un bambino e un ragazzo sono in equilibrio su un'altalena costituita da un'asta di legno appoggiata su un cavalletto, che funziona da "fulcro". Il peso dei due è di 45 kg e 62 kg. La distanza tra loro è di 5 metri. Dove è collocato il cavalletto? [nella figura seguente AB = 5 m, P1 = 45 kg, P2 = 62 kg] Utilizza lo script "baricentro1" presente QUI.

Occorre che AC · P1 = BC · P2, ovvero che il "momento" a sinistra eguagli quello a destra.
Utilizzando lo script:

Il programmino mi fornisce AC = 2.897196261682243 m e, quindi, BC = 5-2.897196261682243 m.
Ovviamente devo arrotondare questi risultati tenendo conto che i pesi erano approssimati (i pesi indicati potrebbero in realtà essere mezzo chilogrammo in più o in meno; poi, in ogni caso, la posizione del cavalletto mi basterebbe conoscerla approssimata ai centimetri).
In conclusione, il cavalletto è posizionato in un punto C distante 2.90 metri, ossia 290 centimetri, da A e 210 centimetri da B.
Controlliamo quanto trovato calcolando il momento a sinistra e quello a destra:
290·45 = 13050, 210·62 = 13020. OK (la piccolissima differenza è dovuta alle approssimazioni).