Osservate la animazione a cui si accede cliccando  QUI  in cui si fa capire che ogni triangolo inscritto in un semicerchio è rettangolo.  Prova a spiegare a parole il ragionamento illustrato dalla animazione.

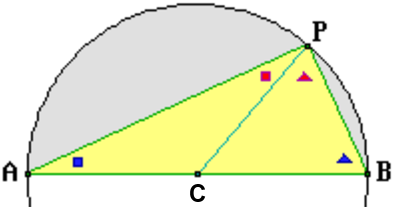
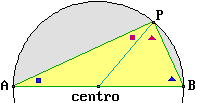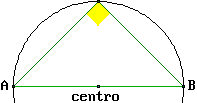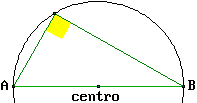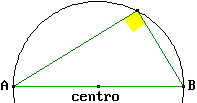
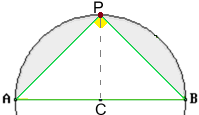
L'animazione, riprodotta qui a sinistra, fa a vedere che un triangolo che abbia un lato coincidente col diametro di un cerchio e l'altro vertice che si muove lungo cerchio deve per forza essere rettangolo.  Nel caso in cui questo vertice sia collocato al centro del semicerchio, come nella figura qui a destra, la cosa sembra evidente:  PAC e PCB sono due mezzi quadrati. La motivazione per cui ciò accade in generale è che i due triangoli con un vertice nel centro C, un altro nel punto P e il terzo in un caso in A e nell'altro in B sono entrambi isosceli in quanto hanno due lati uguali (sono dei raggi). Quindi gli angoli ∠CAP e ∠APC (indicati con due quadratini) e gli angoli ∠PBC e ∠CPB (indicati con due triangolini) sono uguali. La somma dei quattro angoli è pari alla somma degli angoli del triangolo, ossia 180°. Quindi l'ampiezza dell'angolo di vertice P, formato da un angolo-quadretto e un angolo-triangolino, è di 90°.