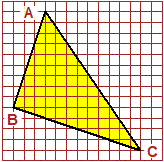
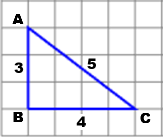
Sul foglio quadrettato riprodotto è disegnato un triangolo. So che il segmento AB è lungo 13.4 cm. Non dispongo di un righello graduato.  (1) Che cosa posso dedurre sulla lunghezza degli altri due lati del triangolo? (2) E se invece, di fronte a un disegno dalla stessa forma ma su un foglio con quadretti di dimensioni diverse, sapessi che AC è lungo 24.7 cm, che cosa potrei dedurre sulla lunghezza degli altri lati del triangolo?

(1)  Noto che il triangolo è rettangolo in B:  come si vede bene nella figura qui a destra, vado da B a A in modo che avanzando verso destra di 1 quadretto avanzo verso l'alto di 3;  vado da B a C in modo che avanzando verso destra di 3 quadretti avanzo verso il basso di 1. Dalla stessa figura ricavo anche che  BC/AB = 4/3.  Dunque BC = AB·4/3 = 13.4·4/3 cm = 17.8666… cm = 17.9 cm. Ho arrotondato ai millimetri, dato che AB era arrotondato ai millimetri. Per trovare AC posso usare il teorema di Pitagora, per il quale AC² = AB²+BC². Evitiamo di scrivere le unità di misura. AC² = 13.4² + (13.4·4/3)² = 13.4² + 13.4²·(4/3)², che potrei riscrivere 13.4²·(1 + (4/3)²) = 13.4²·(1 + 16/9) = 13.4²·25/9, da cui AC = √( 13.4²·25/9 ) = 13.4·5/3 = 22.333333... = 22.3 (cm).

Per inciso, osserviamo che se AB e BC sono lunghi, rispettivamente, 3 e 4 volte un segmento fissato, il triangolo rettangolo ABC deve avere l'ipotenusa AC lunga 5 volte il segmento fissato, in quanto la somma dei quadrati di 3 e di 4 mi dà proprio il quadrato di 5. Quindi avrei potuto trovare AC direttamente come 5/3 di AB:  AC = 13.4·5/3 cm = 22.333… cm = 22.3 cm Volendo, si può utilizzare il programmino "calcoli" presente QUI, nel quale la radice quadrata e l'elevamento a potenza sono indicate con "sqrt" (da "square root") e pow(….…) (da "power"), con davanti "Math": Math.sqrt( Math.pow(13.4, 2) + Math.pow(13.4 * 4/3, 2) ) = 22.333333333333

(2)  Posso, senza usare il teorema di Pitagora, fare direttamente:
AB = 24.7·3/5 cm = 14.82 cm = 14.8 cm;  BC = 24.7·4/5 cm = 19.76 cm = 19.8 cm.