
| Due località A e B sono separate da un fiume. Viene deciso di congiungere A e B con una strada, comprendente un ponte, che, per motivi tecnici, deve essere costruito perpendicolarmente al corso del fiume, in una della 4 collocazioni raffigurate a destra. Cercate di capire dove deve essere collocato il ponte per rendere A e B raggiungibili lungo la strada con il percorso più breve, e di spiegare la motivazione della vostra scelta [supponiamo che i quadretti abbiano il lato che rappresenta 100 metri]. |  |
 |
Il quesito può essere affrontato da soli o, come suggerisce la sua formulazione in 2ª persona plurale, da gruppi di alunni.
Le strategie possono essere varie. Si può provare a calcolare le lunghezze con la calcolatrice:
(1) 10+√(9+36) = 16.708..., (2) √(4+36)+4+√(16+9) = 6.324...+9 = 15.324..., (3) √(16+36)+4+√(4+9)
= 14.816..., (4) √(36+36)+7 = 15.485..., da cui risulta che (3) è la scelta conveniente. Ma si può cercare
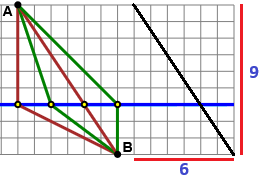
una scelta meno "calcolistica": tenendo conto che la lunghezza del ponte è uguale in tutti i casi, si può alzare la figura nel modo
illustrato qui a sinistra, come se non ci fosse il fiume. A questo punto risulta "evidente" che la scelta (3) è la migliore. Volendo calcolare la lunghezza del ponte, possiamo fare i calcoli usando il teorema di Pitagora: |
La figura è stata tracciata con questo script.