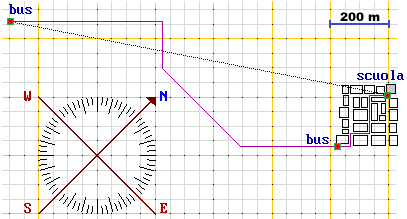


Pierino a scuola non riesce bene in matematica, ma, quando è motivato, cerca di imparare e usare gli strumenti matematici che gli consentono di risolvere qualche problema che lo interessa. Un giorno, dato che a scuola ci deve andare, decide almeno di valutare (tenendo conto di tempi di attesa, strada da percorrere, soldi risparmiabili, …) se gli conviene andare a piedi o in bus. Nel fare questi conti, usando la cartina riprodotta sopra, in cui abbiamo segnato anche le fermate del bus vicine a casa e a scuola, si mette anche a calcolare la strada che gli rimarrebbe da percorrere a piedi nel caso prendesse il bus e quella che percorrerebbe se tagliasse per i campi (Pierino sta in una casa di campagna, vicina alla fermata del bus; il territorio è pianeggiante; in campi non sono cintati e non presentano ostacoli). Non trova la riga graduata, ma ha la calcolatrice. Come può procedere? Fai anche tu altrettanto.
Usando il reticolato si possono trovare gli avanzamenti in orizzontale e in verticale:
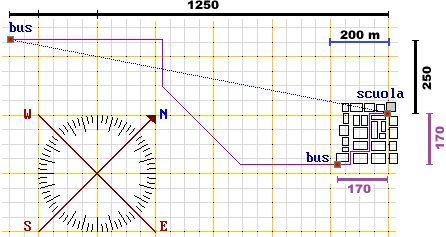
Nel caso del percorso lungo i campi, che più o meno è rettilineo, si può osservare (figura sotto a sinistra)
che è l'ipotenusa di un triangolo rettangolo avente i cateti lunghi 1250 m e 250 m.
La sua lunghezza in metri è

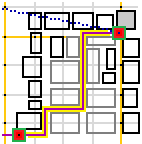
Per la strada bus-scuola si può osservare (figura sopra a destra) che le vie sono tutte orizzontali o verticali per cui la strada da percorrere è comunque la somma dei tratti orizzontali e di quelli verticali, La somma dei tratti orizzontali è 170 metri, ed anche la somma di quelli verticali è 170 metri, per cui la strada bus-scuola è lunga 340 metri.
Anche senza usare il teorema di Piatgora si poteva trovare l'ipotenusa usando il programmino "tri lato-ang-lato" accessibile da questo sito:
