Come posso spezzare in due parti un bastoncino lungo 10 cm in modo che il prodotto delle loro lunghezze sia massimo?  Ovvero, qual è il rettangolo  (figura gialla a destra)  di area massima che abbia due lati le cui lunghezze abbiano somma di 10 cm? Provate a rispondere osservando le due figure  (che cosa rappresenta quella a destra?). Poi giustificate questa risposta.

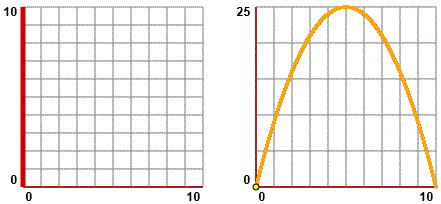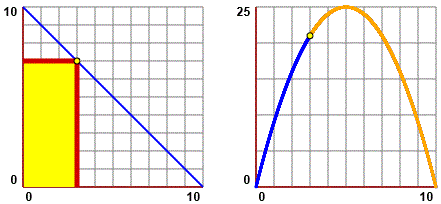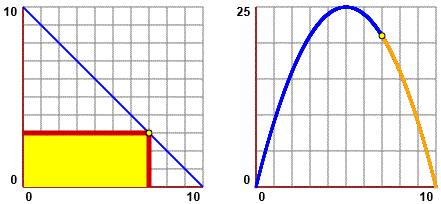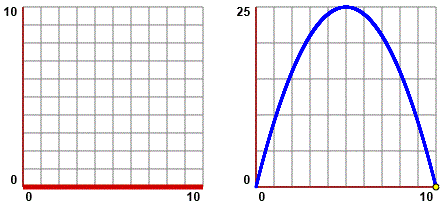
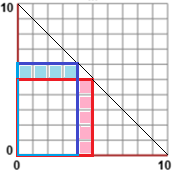
È un quesito (affontabile alla fine della scuola secondaria di 1° grado) da proporre all'intera classe o a gruppi di lavoro.  Occorre osservare che la figura sopra a sinistra rappresenta la relazione tra i due lati del rettangolo, e il rettangolo stesso.  Occorre capire che quella a destra rapprresenta come via via varia il valore dell'area del rettangolo.  Si intuisce e si capisce, con ragionamenti che lì per lì non è facile esprimere a parole, che l'area è massima quando i due lati sono di uguale lunghezza (5 cm). Per mettere meglio a fuoco ed esprimere il ragionamento si può procedere ad esempio così, facendo riferimento alla situazione illustrata qui a sinistra: il rettangolo non quadrato (celeste) ha un rettangolino 4×1 in più e un rettangolino 1×5 in meno del quadrato (rosa), quindi ha area più piccola. Il ragionamento può essere riprodotto in modo del tutto analogo nel caso di ogni altro rettangolo tra quelli considerati nel quesito.