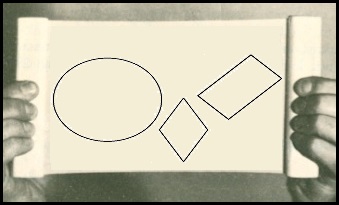
Pendiamo una tela elastica e disegnamoci sopra, come nella figura a fianco, un cerchio, un rettangolo e un rombo con le diagonali una orizzontale e l'altra verticale.  Se stiro la tela il cerchio, il rettangolo e il rombo rimangono tali o cambiano aspetto e, eventualmente, che cosa diventano?

Nel rettangolo i lati rimangano paralleli tra loro ma gli angoli cambiano ampiezza: il rettangolo diventa un parallelogramma non rettangolo.  Nel rombo le diagonali rimangono una perpendicolare all'altra e i lati vengono tutti ingranditi allo stesso modo: il rombo rimane un rombo.  Il cerchio viene dilatato orizzontalmente ma non verticallemente: cambia aspetto; la figura che si ottiene si chiama ellisse.

E se il rombo non fosse disposto con le diagonali orizzontale e verticale? Basta pensare, per esempio, ad un quadrato con i lati orizzontali e verticali (come quello, verde, nella figura seguente): esso viene trasformato in un rettangolo non quadrato, che non è un rombo.

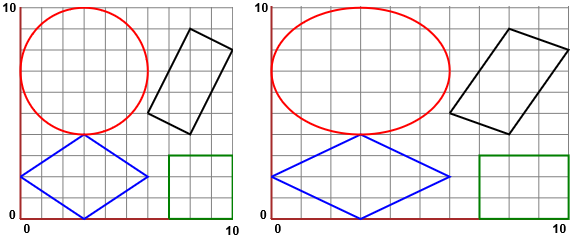
Di queste figure posso determinare anche l'area: è quella della figura iniziale moltiplicata per il numero che per cui è stata moltiplicata la lunghezza della tela elastica. Ad esempio se aumento del 3/7 (circa del 43%) la lunghezza di questa, l'area dell'ellisse è 3/7 in più (ossia circa il 143%) dell'area del cerchio iniziale.

Le figure precedenti sono state tracciate con due script, uno e due:

...
aX = 0; bX = 14; aY = 0; bY = 14
Dx = 1; Dy = 1
titolo = ""
Cax="brown"; Cgr="grey"
quadro=1
C0="blue"; C1="green"; C2="black"; C3="red"
L0x=[0,3,6,3,0]; L0y=[2,0,2,4,2]
L1x=[7,10,10,7,7]; L1y=[0,0,3,3,0]
L2x=[6,8,10,8,6]; L2y=[5,4,8,9,5]
L3x=[]; L3y=[]; H = 2*Math.PI/200
for(i=0;i<=200; i=i+1) {L3x[i]=3+3*Math.cos(H*i); L3y[i]=7+3*Math.sin(H*i)}
...

...
aX = 0; bX = 10; aY = 0; bY = 14
...