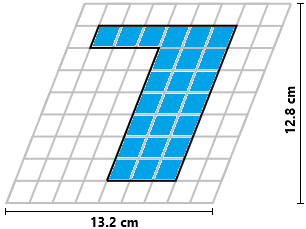
Sapendo che il reticolato raffigurato a destra è largo 13.2 cm ed alto 12.8 cm,  trova l'area della figura (a forma di "sette") disegnata in esso.

Basta che trovi l'area dell'intero reticolato e poi la moltiplichi per il rapporto tra la quantità dei "quadretti" colorati e il totale dei "quadretti", che in realtà "quadretti" non sono, ma hanno la forma di "parallelogrammi".  I "quadretti" sono in tutto 9·9 = 81.  Quelli colorati sono 7·3 + 3 = 8·3 = 24.  L'area dell'intero reticolato è 13.2 cm · 12.8 cm (= 168.96 cm²). Quindi l'area della figura è 24/81·13.2·12.8 = 50.06222 cm² che arrotondo a 50 cm².
Sarebbe stato un po' "stupido", e molto più complicato, fare il calcolo trovando le misure dei vari elementi della figura.

Nota. Volendo trovare l'area tenendo conto delle approssimazioni avrei dovuto considerare che la base (in cm) è compresa tra 13.15 e 13.25 e l'altezza tra 12.75 e 12.85, trovando:
49.67778 cm² = 24/81*13.15*12.75 cm² ≤ area ≤ 24/81*13.25*12.85 cm² = 50.44815 cm²
Quindi è stato sensato prendere 50 cm² come valore dell'area, e non un valore con più cifre.

Se il docente è interessato, ecco lo script con cui è stata realizzata la figura.