• quanto è lungo lo spago? • quanto distano i due paletti? • quanto è larga e quanto è alta l'aiuola?

|
A destra vedete come un giardiniere traccia un'aiuola usando uno spago. Forse avrete anche voi provato a tracciare una curva di questo tipo. È una ellisse. Aprite questo file. Poi provate a rispondere a queste domande: • quanto è lungo lo spago? • quanto distano i due paletti? • quanto è larga e quanto è alta l'aiuola?  |
 |
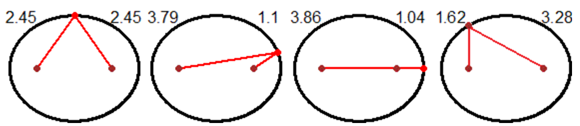
Come potete leggere nella immagine animata, quelle che appaiono sono le lunghezze in metri dei due tratti di spago.
Quindi lo spago è lungo 2.45+2.45 = 4.90 metri. La immagine seguente vi fa capire che i due paletti distano
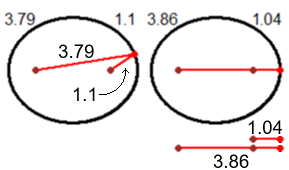
| La larghezza dell'aiuola a questo punto è facile da calcolare:
3.86+1.04 = 3.90 metri. È larga quanto è lungo lo spago! Se ci pensiamo un attimo ce ne convinciamo anche senza calcoli. Per l'altezza dell'aiuola possiamo utilizzare, come si vede nella figura qui a destra, il teorema di Pitagora: il triangolo rettangolo colorato ha ipotenusa lunga 2.45 metri e cateto orizzontale lungo 1.41 metri; quindi il cateto verticale è lungo | 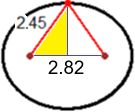 |
Per gli insegnanti. A questo punto (o prima) è bene tracciare in classe delle ellissi come fa il giardiniere della vignetta, con uno spago e due puntine su un pezzo di compensato o di cartone pressato. È poi opportuno vedere che le ellissi possono essere realizzate anche dilatando un telo elastico su cui è stato disegnanto un cerchio o osservando il cerchio tracciato su un vetro o su un pezzo di plastica trasparente che viene ruotato, preannunciando eventualmente che si può dimostrare (ma che non si è in grado ancora di farlo) che anche le figure così ottenute sono delle ellissi, o, viceversa, avendo prima chiamato ellissi i cerchi schiacciati, far vedere che questo è un altro modo per ottenerle.
Per esempi di attività di geometria dinamica "senza computer" vedi gli esempi di materiali costruiti con gli alunni da Emma Castelnuovo.