Da una cartina ricavo che una funicolare ha un percorso rettilineo che si sviluppa orizzontalmente per 845 metri. Su una guida della città leggo che tale percorso ha una inclinazione costante di 25°. Voglio determinare la lunghezza del binario, il dislivello superato dalla funicolare e la pendenza del percorso. Risolvi il problema usando uno dei seguenti programmini (quale?).

   A3    
   |\    
 L2| \ L1
   |  \  
   |___\ 
  A1   L3  A2

   A3    
   |\    
 L2| \ L1
   |  \  
   |___\ 
  A1  L3  A2

   A3    
   |\    
 L2| \ L1
   |  \  
   |___\ 
  A1  L3  A2

   A3    
   |\    
 L2| \ L1
   |  \  
   |___\ 
  A1  L3  A2

   A2    
   |\    
 L3| \ L1
   |  \  
   |___\ 
  A1  L2  A3

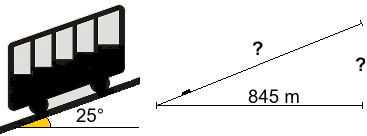Siamo di fronte a un triangolo rettangolo di cui conosciamo un cateto e l'angolo tra questo cateto e l'ipotenusa.  Possiamo usare il programmino "cateto1 angolo".

La strada percorsa (ossia la lunghezza del binario) è l'ipotenusa L1, ossia 932.354...m.  Il dislivello superato è il cateto L2, ossia 394.029...m.
Arrotondo ai metri. Dislivello = 394 m. Percorso = 932 m.

La pendenza è L2/L3 = 394.0299711409665/932.3543415233024 = 0.422618261741. Arrotondando la pendenza è 0.42, ovvero 42%.  La divisione conviene farla sui dati non arrotondati e alla fine arrotondare il risultato.