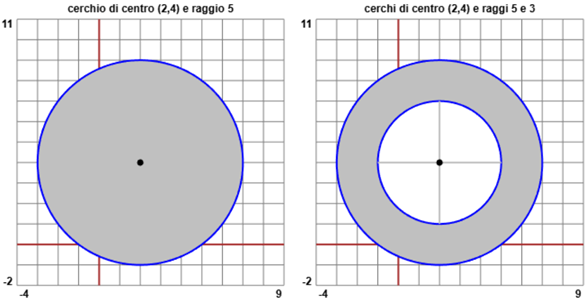
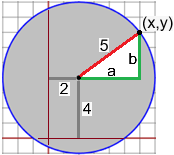
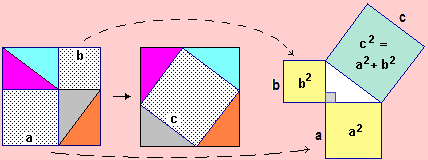
La prima figura qui a destra ha come centro il punto (2,4) e come raggio 5.  È costituita da tutti i punti che distano al più 5 dal punto (2,4).  Potremmo decriverla come l'insieme dei punti (x,y) tali che: (x − 2)2 + (y − 4)2 ≤ 25 Perché?  (ricorda il "teorema di Piatagora) Come potremmo descrivere, sia a parole che con simboli, la seconda figura?

Ricordiamo il teorema di Pitagora.     Se taglio  (nel modo indicato nella prima figura fianco)  un quadrato e ridispongo i quattro triangoli ottenuti come nella figura al centro, mi convinco che i due quadrati di lati a e b occupano in tutto un'estesione equivalente a quella occupata dal quadrato di lato c.     Il lato c non è altro che l'ipotenusa (cioè il lato opposto all'angolo retto) di un triangolo rettangolo avente come cateti (gli altri due lati) a e b.     Dunque:  a2 + b2 = c2

Nel nostro caso (vedi la figura a destra) abbiamo  a2 + b2 = 25  dove  a = x−2  e  b = y−4,  Quindi il bordo del cerchio è descrivibile con la formula: (x − 2)2 + (y − 4)2 = 25 e l'intero cerchio con la formula: (x − 2)2 + (y − 4)2 ≤ 25

    La seconda figura è data dal precedente cerchio da cui è stato tolto il cerchio con lo stesso centro e di raggio 3, ossia il cerchio:

    Posso descrivere la figura come l'insieme dei punti (x,y) tali che: