Il rettangolo disegnato a fianco può essere descritto così:
[ "≤" significa "è minore o uguale a" ]
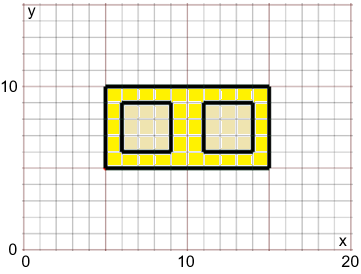
Come possono essere descritti i due quadrati?
Il rettangolo disegnato a fianco può essere descritto così: [ "≤" significa "è minore o uguale a" ] Come possono essere descritti i due quadrati? |
 |
Quadrato a sinistra: 6 ≤ x ≤ 9, 6 ≤ y ≤ 9.
Quadrato a destra: 11 ≤ x ≤ 14, 6 ≤ y ≤ 9.
Invece il rettangolo senza i due quadrati potrei descriverlo così:
La figura è stata realizzata con questo
programmino (che puoi trovare anche qui, col nome "lapis")
con i comandi:
11111 11111 22222 33333 33333 44444 0 ab 111 222 333 444 0 aaaaa 111222333444 0
ovvero copiandoli e incollandoli nel riquadro dello script lapisA (che trovi qui).
Nella scuola superiore si vedrà che il rettangolo può essere descritto in forma abbreviata con:
( l'insieme degli (x,y) tali che 5 ≤ x ≤ 15, 5 ≤ y ≤ 10 )
e che il rettangolo meno i due quadrati con:
dove il simbolo "−" può essere letto "meno". Dati due insiemi A e B, con A−B si indica l'insieme degli elementi di A che non sono elementi di B. L'operazione "−" viene chiamata "differenza" o "complemento relativo".