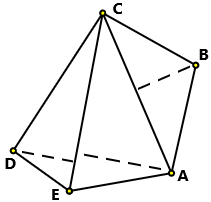
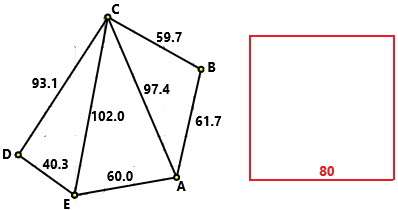
In una particolare zona di campagna i terreni sono suddivisi attraverso dei tratti di corda che congiungono dei pali infissi nel terreno. Giovanni ha il terreno raffigurato a fianco, che, per valutarne il perimetro e l'area, ha suddiso nel modo illustrato. Ha misurato le seguenti distanze: AB = 61.7 m, BC = 59.7 m, CD = 93.1 m, DE = 40.3 m, EA = 60.0 m, EC = 102.0 m, AC = 97.4 Ha misurato poi la distanza di D da CE trovando 36.8 m, quella di A da CE trovando 55.7 m, quella di B da AC trovando 36.2 m. Quanto è esteso il terreno di Giovanni?

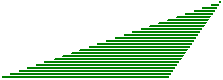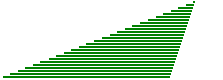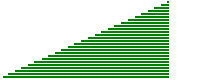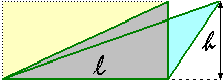Ricordiamo che un qualunque triangolo pu essere trasformato senza cambiarne l'area muovendo un suo vertice parallelamente al lato opposto.  Quindi scelto un lato lungo l come base e chiamata h la altezza che il triangolo ha rispetto ad l,  la sua area è pari a mezzo rettangolo di base l ed altezza h, ossia è pari a l·h/2.

L'area di CDE è il prodotto di EC per la distanza di CE da D. Le misure di ED e di CD (così come quelle degli altri lati del campo) non mi servono per il calcolo dell'area. Quindi:
area di CDE = 102.2·36.8/2 m².  Analogamente:
area di ACE = 102.2·55.7/2 m²,  area di ABC = 97.4·36.2/2 m².
In tutto:  102.2·36.8/2 + 102.2·55.7/2 + 97.4·36.2/2 m².
Mi conviene dividere per 2 tutto alla fine:
(102.2·36.8 + 102.2·55.7 + 97.4·36.2) / 2 m².
Faccio i calcoli con la calcolatrice e poi controllo la sensatezza del risultato:  6489.69 m²
Dato che i dati che ho moltiplicato erano arrotondati a 3 cifre, arrotondo a 3 cifre anche il risultato (le cifre finali non sono affatto significative).  Per altro non mi serverebbe a niente conoscere molte cifre del valore dell'area. Prendo quindi: 6490 m².
Volendo, usando l'ara come unità di misura (1 ara = 100 m²) posso dire che il terreno ha un'estensione di 64.9 are, o, più semplicemente, di 65 are.

L'area di 6400 m² corrisponde ad un quadrato di lato 80 m:  l'ordine di grandezza del risultato trovato è sensato. Vediamo infatti che il nostro campo è confrontabile con un quadrato di queste dimensioni.

Volendo, capito che l'area di un triangolo su una superficie piatta dipende solo dalle dimensioni dei lati, si può poi usare a "scatola nera" (controllandone prima l'esito su triangoli semplici tracciati sulla carta quadrettata) lo script "tri lato-lato-lato" accessibile online da qui trovando (vedi sotto) 6483.8960650091, che poi arrotondo a 6480.

lati 93.1,40.3,102  area = 1875.7549081902987
lati 60,97.4,102  area = 2843.986449317224
lati 61.7,97.4,59.7  area = 1764.1547075015844
1764.1547075015844+2843.986449317224 = 4608.141156818809
4608.141156818809+1875.7549081902987 = 6483.896065009108