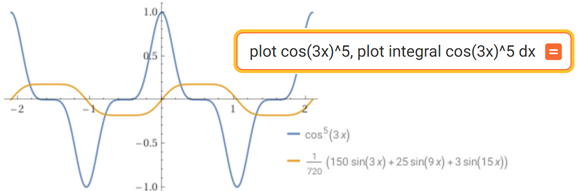
Calcolare    ∫ cos(3x)⁵ dx   (procedere per sostituzione)

t = sin(3x),  dt/dx = cos(3x)·3,  cos(3x)⁴ = (cos(3x)²)² = (1−sin(3x)²)²
1/3·∫ (1 − t²)² dt = 1/3·∫ t⁴ − t² + 1 dt = t⁵/15 − 2·t³/9 + t/3
∫ cos(3x)⁵ dx = sin(3x)⁵/15 − 2·sin(3x)³/9 + sin(3x)/3  (+ c)

Per altri commenti: calcolo di integrali neGli Oggetti Matematici.

Con WolframAlpha posso controllare sia simbolicamente che graficamente il risultato.