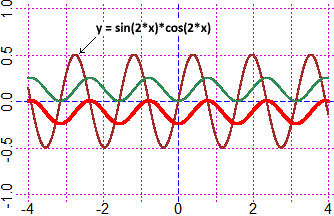
Calcolare    ∫ sin(2x) cos(2x) dx   (procedere per sostituzione)

u = sin(2x),  du = 2 cos(2x) dx,  ∫ u/2 du = u²/4 (+ c)
∫ sin(2x) cos(2x) dx = sin(2x)²/4 (+ c)

Per altri commenti: calcolo di integrali neGli Oggetti Matematici.

Con WolframAlpha [integral sin(2*x)*cos(2*x) dx] ottengo -1/8*cos(4*x), che è equivalente; infatti introducendo
-1/8*cos(4*x) - sin(2*x)^2/4     ottengo  -1/8, ossia una costante (la cui drivata è 0).