Calcola    ∫ √(1 − x²) dx    (procedi con un'opportuna sostituzione trigonometrica)

Pongo √(1 − x²) = cos(θ), ho dx = cos(θ) dθ e mi riconduco a:
∫ √(1 − sin(θ)²) cos(θ) dθ = ∫ cos(θ)² dθ = ∫ (1+cos(2θ))/2 dθ = θ/2 + sin(2θ)/4,  da cui:
∫ √(1 − x²) dx = arcsin(x)/2 + sin(2 arcsin(x))/4 = arcsin(x)/2 + sin(arcsin(x))·cos(arcsin(x)) = arcsin(x)/2 + x·√(1−x²)/2

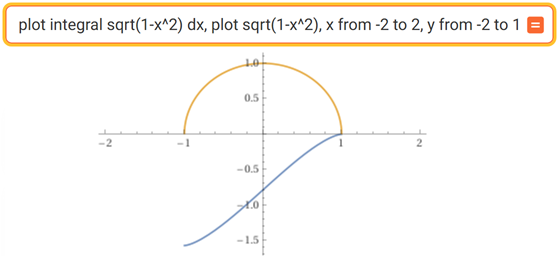
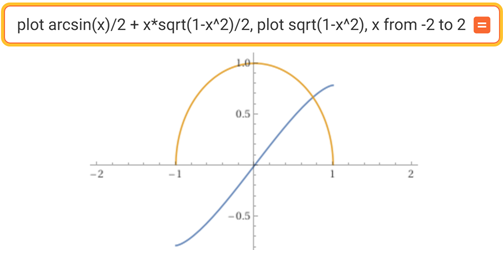
Controllo grafico:

Per altri commenti: calcolo di integrali neGli Oggetti Matematici.