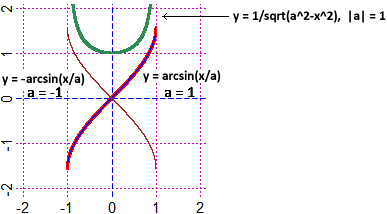
Calcolare    ∫ 1/√(a²−x²) dx   (procedere per sostituzione)

In prima battuta faremmo così:  t = x/a,  dt/dx = 1/a,  dx = a dt
1/a ∫ a/√(1−t²) dt = ∫ 1/√(1−t²) dt
1/3·∫ (1 − t²)² dt = 1/3·∫ t⁴ − t² + 1 dt = t⁵/15 − 2·t³/9 + t/3 = arcsin(t)
∫ 1/√(a²−x²) dx = arcsin(x/a) (+ c)
Tutto sembra tornare, ma in questo calcolo, all'inizio, abbiamo portato fuori la costante a dalla radice supponendo che fosse positiva.  Nel caso in cui a sia negativo otteniamo (con calcoli analoghi o, direttamente, ragionando):
∫ 1/√(a²−x²) dx = −arcsin(x/a) (+ c)
Nel caso in cui a sia nullo l'integranda non è definita.

Con WolframAlpha ottengo il termine equivalente: arctan(x/sqrt(a^2-x^2))   Per altri commenti: calcolo di integrali neGli Oggetti Matematici.