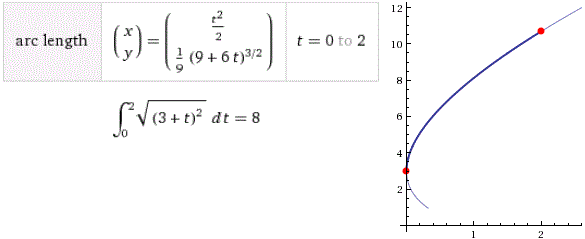La lunghezza, da t=0 a t=2, dell'arco di curva di equazioni parametriche x = t²/2, y = (6t+9)^3/2/9 è:
    A) 10    B) 12    C) 8    D) 14

Facciamo subito i conti con WolframAlpha, e poi ragioniamoci:
arc length of ( t^2/2, (6*t+9)^(3/2)/9 ) from t=0 to 2

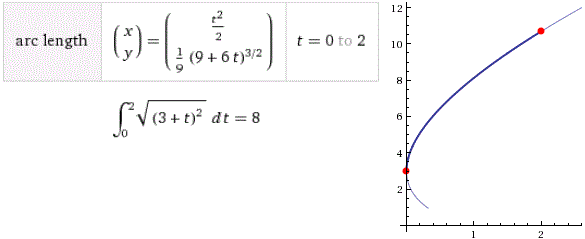
La risposta corretta è C e schizzando il grafico della curva, che va da (3,0) a, circa (2,10.7), possiamo approssimare l'arco con un segmento lungo √(8^2+2^2), ossia circa 8 (10 sarebbe decisamente troppo grande). Proviamo a capire come è stata ottenuta la soluzione fornita, assieme alle considerazioni svolte qui.
Posto x = f(t), y = g(t),  f'(t) = t, g'(t) = √(6t+9); l'integrale tra 0 e 2 della radice della somma dei loro quadrati è:
∫ _[0,2] √(t²+6t+9) dt = ∫ _[0,2] √((t+3)²) dt = [poiché t+3>0 per t tra 0 e 2]  ∫ _[0,2] t+3 dt = 2²/2+3·2 = 8

I calcoli con lo script:

a=0; b=2
document.write("la lunghezza della curva da t="+a+" a t="+b+"<br>")

function x(t) {return t*t/2}
function y(t) {return Math.pow(6*t+9,3/2)/9}
n = 1e4; rip=6
for(k=1; k<=rip; k=k+1) {  n=n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+", L = "+L+"<br>")  }

la lunghezza della curva da t=0 a t=2
la lunghezza della curva da t=0 a t=2
n = 20000, L = 7.999999999859822
n = 40000, L = 7.9999999999649045
n = 80000, L = 7.999999999991316
n = 160000, L = 7.99999999999792
n = 320000, L = 7.999999999999505
n = 640000, L = 7.999999999999726

Per altri commenti: Altri usi degli integrali neGli Oggetti Matematici.