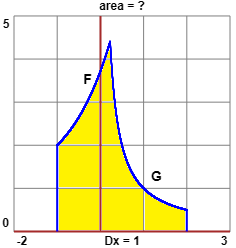
Calcola l'area della figura evidenziata a fianco, dove i grafici tracciati parzialmente sono quelli delle funzioni F: x → exp(x+1)+1 e G: x → 1/x. Aiutati col computer per determinare dove essi si intersecano.

Capisco dal grafico che l'area è circa 6 "quadretti", ovvero circa 6.
I due grafici si incontrano quando exp(x+1)+1 = 1/x.  Determinio l'intersezione con, ad esempio, WolframAlpha:
solve exp(x+1)+1 = 1/x for x   →   x ≈ 0.22675064483434807830
Già che ci siamo calcoliamo anche l'area, che poi determineremo anche "a mano":
integrate exp(x+1)+1 from -1 to 0.226750645   →   ≈ 3.63688
integrate 1/x from 0.226750645 to 2   →   ≈ 2.17705
3.63688+2.17705   →   5.81393   in accordo con la stima iniziale
Procedendo "a mano":
q = 0.2267506448343480783     ∫ _[−1,q] F + ∫ _[q,2] G = (*)
∫ exp(x+1)+1 dx = exp(x+1)+x [più eventuali costanti]
∫ 1/x dx = log(x) [più eventuali costanti]
(*) = exp(q+1)+q−exp(0)+1+log(2)−log(q) =5.81393295964913217...