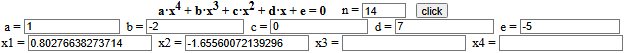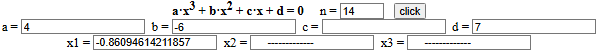Data la funzione x → x⁴ − 2x³ + 7x − 5, studiane l'andamento, compresa la concavità, eventualmente trovando alcuni valori (zeri o punti di massimo o minimo o …) in forma approssimata.

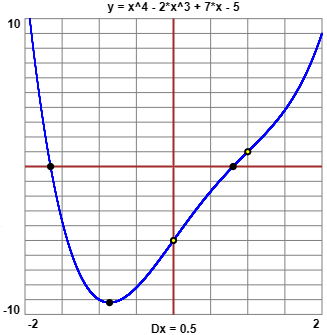
Si tratta di una funzione polinomale di grado pari e di coefficiente direttivo positivo, quindi per l'input che tende a ∞ o a −∞ tende a ∞. Potrebbe avere da 0 a 4 zeri. Se disponiamo di un computer possiamo facilmente stabilire che l'andamento è quello rappresentato a fianco. Altrimenti la cosa più semplice è determinare le sue derivate. Indichiamo con F la funzione:  F '(x) = 4x3−6x2+7, F "(x) = 12x2−12x = 12x(x−1).  F "(x) = 0 sse x=0 o x=1.  F '(0) = 7,  F '(1) = 5;  quindi in 0 e in 1 abbiamo flessi ascendenti (vedi i pallini gialli).  Le ordinate corrispondenti sono F(0) = −5, F(1) = 1.  Quindi possiamo schizzare un grafico simile a quello a fianco. Volendo trovare con più precisione le coordinate dei punti in cui il grafico taglia l'asse x e in cui raggiunge il punto più basso (vedi i pallini neri) possiamo procedere per tentativi ragionati, o usare un programma per la ricerca degli zeri. QUI lo script con cui si può tracciare il grafico a destra.  Sotto l'impiego dello script "equazioni" presente QUI per risolvere le equazioni polinomiali di 3º e 4º grado sopra considerate,  e dello script "calcolatrice2" per calcolare l'ordinata del punto di minimo.

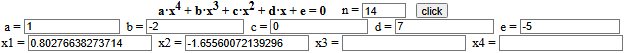
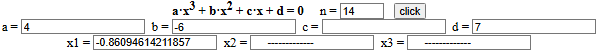
Potevo studiare il problema anche con WolframAlpha introducendo semplicemente x^4 - 2*x^3 + 7*x - 5

In alternativa, senza utilizzare altri software, si poteva utilizzare JavaScript, il linguaggio di programmazione incorporato nei browser (JavaScript).
Gli zeri:

function F(x) {return Math.pow(x,4)-2*Math.pow(x,3)+7*x-5}
a=-2; b=0
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
       m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
       if(y1*y2 > 0) {a = m} else {b = m} }
    document.write(m," ")
}

-1.655600721392961   0.8027663827371372

Per la ricerca del punto di minimo potrei usare un procedimento in qualche modo simile al precedente o utilizzare una ricerca in un dato intervallo generando molti punti a caso in esso, come questa:

if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
       m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
       if(y1*y2 > 0) {a = m} else {b = m} }
    document.write(m,"<br>")
}

Ottengo esiti come i seguenti (ho usato più volte il programmino per comprendere qual è la loro precisione):

Circa: minimo = -9.200888440844139 per x = -0.8609461516418309
Circa: minimo = -9.200888440844139 per x = -0.8609461351118091
Circa: minimo = -9.200888440844139 per x = -0.8609461344953472
Circa: minimo = -9.200888440844139 per x = -0.8609461545869073

Posso prendere  x = -0.86094614,  f(x) = -9.200888440844139

Richiami:   concavità di una funzione  neGli Oggetti Matematici.