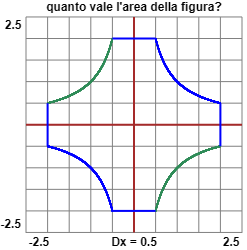
Calcola arrotondata a 10 cifre, utilizzando lo script "integrali" presente QUI, l'area della figura racchiusa tra i grafici di x → 1/x e di x → –1/x e le rette x = –2, x = 2, y = –2, y = 2.

L'area è composta da un quadrato di area 4 e 8 superfici uguali di area: ∫_I1/x dx con I = [1,2]. Calcolo questo integrale con lo script:

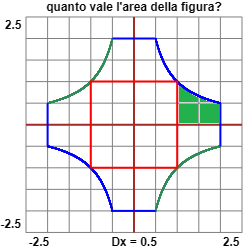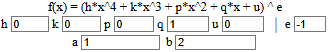n = 10000   I = 0.6931471802474457
n = 100000  I = 0.6931471805568251
n = 500000  I = 0.6931471805598186

Arrotondando a 11 cifre, 0.69314718056. Quindi l'area complessiva (usando ad es. una delle calcolatrici presenti nello stesso file) è 4+8*0.69314718056 = 9.54517744448 = 9.545177445 (arrotodameno a 10 cifre)
Facciamo un controllo intuitivo: la figura di cui ho calcolato l'area 0.693… è circa un quadrato di area 1 meno una fetta pari a un po' più di 1/4; quindi l'area dovrebbere essere un po' meno di 1-0.25 = 0.75: OK.