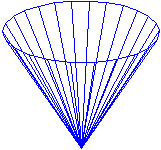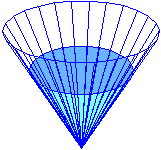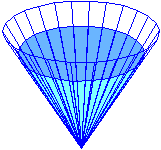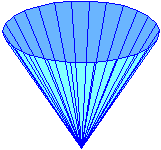
In un recipiente di forma conica viene introdotta dell'acqua.  Il rubinetto da cui esce l'acqua ne fa uscire un filo, a velocità costante.  Il livello dell'acqua sale a velocità costante o no?  Perché?

Come si vede nell'immagine, l'acqua del cono all'inizio sale più rapidamente, poi man mano diminuisce la velocità di salita.  Perché?
Qui sotto sono raffigurati tre istanti: quando il recipiente è ancora vuoto, quando il livello dell'acqua ha raggiunto mezza altezza e quando il recipente è pieno.

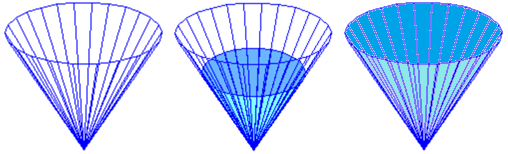
Si capisce facilmente che lo spazio occupato dall'acqua quando viene raggiunta mezza altezza è molto minore dello spazio ancora da riempire.  La spiegazione "matematica" è abbastanza semplice: il volume del cono è un terzo del prodotto tra area di base (che in questo caso è in alto) e altezza, e se raddoppio l'altezza anche il diametro raddoppia. Il cono sulla destra ha altezza doppia del cono al centro ma ha volume più che doppio in quanto anche l'area di base è aumentata.

Di quanto è aumentata? Il raggio è raddoppiato quindi l'area di base è quadruplicata.  Qundi il volume dell'intero cono è il quadruplo di quello con altezza dimezzata, non il doppio.