y = A x3 + B x2 + C x + D
f(1)=2 AND f(2)=1 AND f'(1)=0 AND f'(2)=0, ossia:
A+B+C+D=2 AND 8A+4B+2C+D=1 AND 3A+2B+C=0 AND 12A+4B+C=0
Si ottiene: A = 2, B = -9, C = 12, D = -3
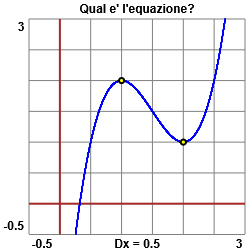
| Determinare A, B, C e D in modo che la curva disegnata a fianco abbia equazione: y = A x3 + B x2 + C x + D | |
|
Se indichiamo con f(x) il termine A x3 + B x2 + C x + D, si tratta di risolvere rispetto ad {A,B,C,D} il sistema (ottenuto imponendo che il grafico passi per i punti (1,2) e (2,1) e ivi abbia tangente orizzontale): f(1)=2 AND f(2)=1 AND f'(1)=0 AND f'(2)=0, ossia: A+B+C+D=2 AND 8A+4B+2C+D=1 AND 3A+2B+C=0 AND 12A+4B+C=0 Si ottiene: A = 2, B = -9, C = 12, D = -3 |
|
A+B+C+D=2 8A+4B+2C+D=1 3A+2B+C=0 12A+4B+C=0 |
A+B+C+D=2 2A+D=1 3A+2B+C=0 6A-C=0 |
5A+B=1 D=1-2A 9A+2B=0 C=6A |
B=1-5A D=1-2A 9A+2-10A=0 C=6A |
B=-9 D=-3 A=2 C=12 |
| sottratte 3ª*2 a 2ª e a 4ª |
sostituite C e D in 1ª e 3ª |
sostituita B in 3ª |
sostituita A in 1ª,2ª e 4ª |
Per altri commenti: 
derivata e differenziale e sistemi di equazioni neGli Oggetti Matematici.
Posso controllare la risposta con lo script online "sistemi equazioni" presente QUI:
