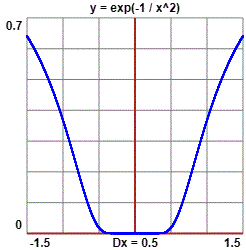
Sia G la funzione ottenuta prolungando con continuità nell'origine la funzione x → e^–1/x2.
Esiste G'(0)? In caso negativo motivare la risposta, in caso affermativo determinarne il valore.
Stessi quesiti per G"(0).

e^–1/x2 equivale a 1/e^1/x2
per x → 0  –1/x² → –∞, e quindi e^–1/x2 → 0.
Quindi G(0)=0
d(e^–1/x2)/dx = 2e^–1/x2/x² → 0 per x → 0.
Infatti e^t per t→∞ è un infinito di ordine superiore rispetto a t^α per ogni α>0, per cui e^1/u per u→0+ è un infinito di ordine superiore rispetto a 1/u^α, per cui 1/e^1/u per u→0+ è un infinitesimo di ordine superiore rispetto a u^α. E in particolare (per u=x² e α=1) e^–1/x2 è d'ordine superiore rispetto a x² per x→0 (non serve "0+" in quanto x²≥0).
Quindi G'(0)=0
d²(e^–1/x2)/dx² = d(2e^–1/x2/x²)/dx = -2e^–1/x2(3x²-2)/x⁶ ≈ 4e^–1/x2/x⁶ → 0 per x → 0 per quanto visto sopra.
Quindi G"(0)=0

Tracciando il grafico al computer (vedi) risulta subito evidente la velocità con cui esso si "appiattisce" avvicinandosi all'origine.