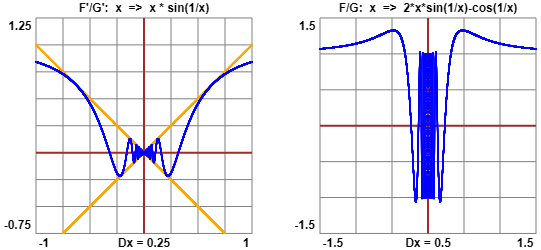
Siano F(x) = sin(1/x)·x² e G(x) = x. Determinare F'(x) e G'(x) e studiare il limite di F'(x)/G'(x) per x che tende a 0. Valutare, tenendo conto di quanto ottenuto, i rischi di una interpretazione scorretta del teorema de L'Hopital.

F'(x)/G'(x) = 2x sin(1/x)−cos(1/x) non ha limite per x che tende a 0 mentre F(x)/G(x) tende a 0, in quanto |F(x)/G(x)| = |sin(1/x)·x| ≤ |x| → 0.
L'implicazione inversa della regola de L'Hopital non vale!

Per il teorema de L'Hopital vedi Proprietà delle funzioni continue e di quelle derivabili neGli Oggetti Matematici.

I grafici sono stati realizzati con questo e questo script.