Per studiare sperimentalmente  lim_x→0 sin(x)/x  si può studiare  sin(1)/1 = 0.8414709..., sin(0.1)/0.1 = 0.998334..., sin(0.01)/0.01 = 0.999983..., ossia il limite per n → ∞ di  sin(x(n))/x(n)  avendo preso una successione x(n) che tende a 0 per n → ∞.  In generale, per studiare sperimentalmente lim_x→α F(x) si può studiare lim_n→∞ F(x(n)) se x(n) → α.  Ad esempio se α è ∞ si possono calcolare F(1), F(10), F(100), F(1000), …
    Rifletti sull'attenzione con cui si usare questo metodo cercando di trovare, se è possibile farlo, almeno un esempio di:
(1) una funzione F, un numero L e una successione x(n) divergente a ∞ tale che F(x(n)) → L per n → ∞ e F(x) per x → ∞ non abbia limite;
(2) una funzione F e una successione x(n) divergente a ∞ tale che F(x(n)) → ∞ per n → ∞ e F(x) per x → ∞ non abbia limite;
(3) una funzione F, due numeri p ed L e una successione x(n) convergente a p tale che F(x(n)) → L per n → ∞ e F(x) per x → p non abbia limite;
(4) una funzione F, due numeri p ed L e una successione x(n) convergente a p tale che F(x) per x → p tenda a L e F(x(n)) per n → ∞ abbia limite diverso da L.

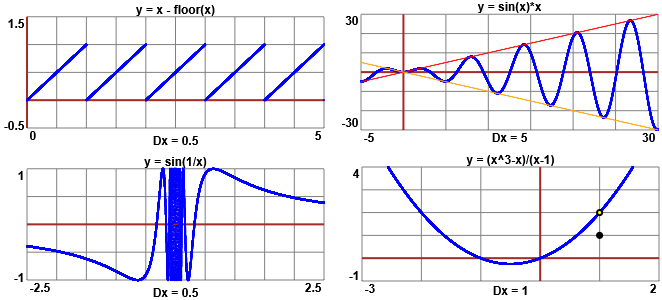
(1) Se, ad es., F è una funzione periodica non costante di periodo T, k è un qualunque numero e x(n) è la successione (divergente a ∞) n → k+nT, allora F(x(n)) vale costantemente f(k) e quindi converge a tale valore; mentre il limite di F(x) per x → ∞ non esiste.  Sopra è raffigurato il caso di  F: x → x - floor(x)  ("floor": funzione parte intera); se x(n)=n F(x(n))=0 [ossia F(0)=F(1)=F(2)=…=0], se x(n)=n+0.5 F(x(n))=0.5 [ossia F(0.5)=F(1.5)=…=0.5].

(2) Posso prendere F(x) = x·G(x) con G(x) periodica e k tale che G(k) > 0, e, se T è il periodo, x(n) = k+n·T.  Sopra è raffigurato il caso di G: x → sin(x), in cui T = 2π.  Se prendo x(n) = π/2+2nπ, F(x(n)) = x(n)·sin(π/2) = x(n) → ∞  (se prendessi x(n) = nπ avrei F(x(n)) = 0 → 0),  mentre F(x) per x → ∞ non ha limite.

(3) Nel caso di F(x) = sin(1/x) se prendo la successione x(n) decrescente formata dagli input positivi per cui F vale 1 (sono le ascisse dei punti in cui il grafico è tangente alla semiretta y=1 AND x>0), x(n) tende a 0, F(x(n)) è uguale costantemente, e quindi convergente, a 1, mentre F(x) per x → 0+ non ha limite;

(4) Nel caso di F(x) = (x³-x)/(x-1), con F(1) = 1, per x → 1 F(x) → 2 mentre se x(n) vale costantemente 1 si ha che F(x(n)) = F(1) = 1 → 1.

    Quindi, se si trova che su una successione di valori di x tendente ad α F(x) tende a β, si può congetturare che F(x) tenda a β, ma, per averne la certezza usando questo metodo, bisognerebbe (cosa in genere impossibile) verificare la cosa su tutte le possibili successioni di tal tipo.
    Tuttavia se sappiamo (per qualche considerazione teorica o in base ad altre informazioni) che F(x) ha limite, possiamo concludere che questo limite è β, tranne in casi particolari come quello illustrato in (4), in cui  • α è un numero reale e  • in α F è definita e assume un valore diverso dal limite, e  • la successione x(n) assume infinite volte il valore α.  Solo in casi di questo genere potrebbe anche accadere che F(x(n)) non abbia limite mentre F(x) lo ha.

Per altri commenti: limiti neGli Oggetti Matematici.