Sia F(x) = ⁴√(x²).  Schizza i grafici di F e della sua funzione derivata.

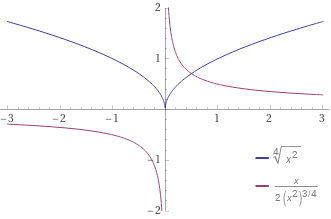
F è definita per ogni input. 4√(x2) = (x2)1/4 = x2·1/4 = x1/2 = √x, ma nella trasformazione abbiamo ristretto il dominio a x≥0. La prima funzione che viene composta (x → x2) ha output uguali per input opposti, ovvero ha grafico simmetrico rispetto all'asse y (in breve: è una funzione "pari"). Quindi F si comporterà simmetricamente (rispetto all'asse y) per x≤0, ossia ivi F(x) = √(–x). Ossia il grafico di F è quello di x → √x unito alla figura ottenuta ribaltando questo attorno all'asse y. Per x>0 F'(x) = (√x)' = 1/(2√x) . Per x → ∞ tende a 0, per x →0+ tende a ∞. A sinistra dell'asse y il grafico di F' è simmetrico (rispetto all'origine): F'(x)→0 per x→-∞, F'(x)→-∞ per x→0-.

In 0 F' non è definita.

Per altri commenti: potenze 2 (per le potenze ad esponente frazionario e i relativi problemi di dominio), funzione 2 (per le funzioni pari) e derivata (per le funzioni continue con punti del grafico senza tangente) neGli Oggetti Matematici.

Il grafico sopra a destra è stato realizzato con WolframAlpha mediante il comando
plot (x^2)^(1/4), D((x^2)^(1/4)), -3 < x < 3, -2 < y < 2