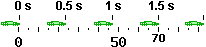
Sotto sono riprodotte le fotografie di un'auto che (inizialmente) viaggia a velocità costante,scattate ogni mezzo secondo a partire da quando l'autista intravede un ostacolo e (con un tempo di reazione 1.5 sec) inizia a frenare (clicca qui se vuoi ingrandire l'immagine).
– Valuta la velocità inziale dell'auto.
– Traccia i grafici della posizione dell'auto e della sua velocità in funzione del tempo (a partire dalla posizione e dall'istante in cui incomincia la frenata).
– Valuta in modo opportuno come varia la velocità al passare del tempo.

Per 1.5 s  (il tempo di reazione dell'autista)  l'auto continua a viaggiare a velocità costante.  In questo tempo percorre circa 70 m, per cui la velocità  (che in questo tratto coincide con la velocità media)  è 70 m / (1.5 s) = 140 m / (3 s) = 47 m/s,  ovvero 140 (km/1000) / (3 h/60·60) = 140·20·60/1000 km/h = 168 km/h.

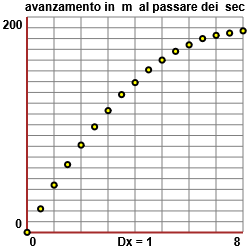
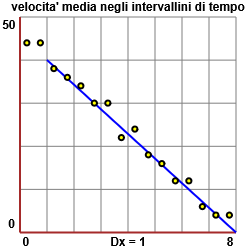
La tabella sotto a sinistra riporta le posizioni dell'auto in funzione del tempo trascorso, misurati a partire da quanto l'autista inizia a frenare  (dopo 1.5 s, a 70 m dalla posizione della prima foto).  Nel grafico a sinistra la tabella è rappresentata graficamente.  Al centro è rappresentata graficamente la velocità media nei vari intervallini di tempo; il grafico oscilla a causa degli errori di arrotondamento  (le differenze tra i tempi e gli spazi calcolate risentono delle approssimazioni dei dati).  Nel grafico a destra è evidenziato che approssimativamente la velocità scende con una pendenza -40/7 ≈ -6.  Possiamo dire che l'auto perde ogni secondo circa 6 m/s di velocità, ovvero che subisce una decelerazione di circa 6 m/s².

t s 0 0 0.5 22 1 44 1.5 63 2 81 2.5 98 3 113 3.5 128 4 139 4.5 151 5 160 5.5 168 6 174 6.5 180 7 183 7.5 185 8 187

I grafici precedenti sono stati tracciati con questi script online:  uno,  due,  tre.  Ma si poteva impiegare altro software.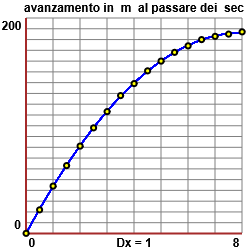
Nel grafico a fianco è tracciata la parabola che approssima i dati, realizzata con lo script online quattro, dove si è utilizzata la funzione polinomiale di 2° grado che approssima i dati i cui coefficienti sono stati ottenuti con lo script "regressione quadratica" presente qui, di cui verrà discussa l'impostazione in una successiva voce ("correlazione tra variabili casuali"):

Si può semplicemente usare anche il software online WolframAlpha. Vedi qui.

quadratic fit {(0,0),(0.5,22),(1,44),(1.5,63),(2,81),(2.5,98),(3,113),(3.5,128),(4,139),(4.5,151),(5,160),(5.5,168),(6,174),(6.5,180),(7,183),(7.5,185),(8,187)}
                  -0.121775 + 46.5121 x - 2.90041 x^2     (e immagine sottostante)

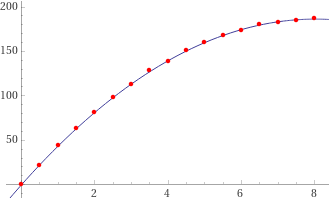
Nota bene. Questi dati si riferiscono a una situazione "buona":  freni efficienti, autista attento e sobrio, strada asciutta, ….  In altre condizioni il tempo di reazione può essere maggiore e il valore assoluto della decelerazione può essere minore, per cui lo spazio di frenata può essere molto maggiore di quello (di circa 250 m) qui indicato.

Per altri commenti: velocità di variazione neGli Oggetti Matematici.